
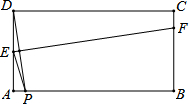
 如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.
如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$. 分析 由要使四边形EPFD为菱形,则需DE=EP=FP=DF,可得当点E与点A重合时,AP最小;当点P与点B重合时,AP最大,继而求得四边形EPFD为菱形的AP的取值范围,进而得到S的取值范围.
解答 解:∵要使四边形EPFD为菱形,则需DE=EP=FP=DF,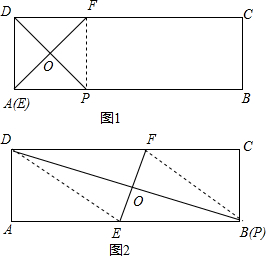
∴如图1:当点E与点A重合时,AP=AD=1,此时AP最小;
此时,S=AP2=1.
如图2:当点P与B重合时,AP=AB=2,此时AP最大;
此时,设AE=x,则EP=DE=2-x,根据勾股定理得:12+x2=(2-x)2,
解得:x=$\frac{3}{4}$,
∴EP=$\frac{5}{4}$,
∴S=1×$\frac{5}{4}$=$\frac{5}{4}$.
∴四边形EPFD为菱形时,S的取值范围:1≤S≤$\frac{5}{4}$.
故答案为:1≤S≤$\frac{5}{4}$.
点评 此题考查了菱形的判定与性质、折叠的性质、矩形的性质以及面积的计算.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
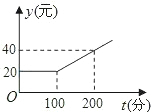 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
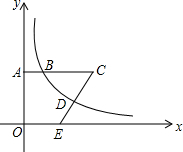 如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.
如图所示的平面直角坐标系xOy,点A在y轴正半轴上运动,点B在第一象限,AB⊥y轴,AB=4,在AB的延长点上取一点C,过点C作直线交过点B的双曲线于点D,交x轴正半轴于点E,且CD=DE,设OA=t,四边形OACE的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
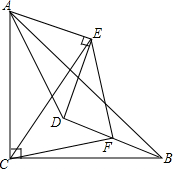 如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.
如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
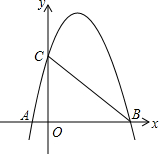 如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).
如图,抛物线与x轴相交于A(-1,0),B(3,0)两点,与y轴相交于点C(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-b+1,a+1) | B. | (-a,-b+2) | C. | (b-1,-a+1) | D. | (a,b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com