
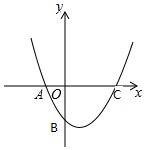
 设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.分析 (1)令x=0,求出与y轴的坐标;令y=0,求出与x轴的坐标;
(2)分三种情况讨论:①当AB为底时,若点D在AB上方;若点D在AB下方;②当AB为腰时,A为顶点时,③当AB为腰时,A为顶点时;仔细解答即可.
(3)当AP+BQ最小时,四边形ABQP的周长最小,根据轴对称最短路径问题解答.
解答 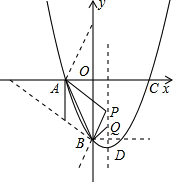 解:(1)当x=0时,y=-$\sqrt{3}$;
解:(1)当x=0时,y=-$\sqrt{3}$;
当y=0时,x=-1或x=2;
则A(-1,0),B(0,-$\sqrt{3}$),C(2,0);
(2)如图,Rt△ABO中,OA=1,OB=$\sqrt{3}$,
∴AB=2,∠ABO=30°,∠BAO=60°,
∴△ABD是顶角为120°的等腰三角形.
①当AB为底时,若点D在AB上方,由∠ABO=∠BAD=30°,AB=2,得D1(0,-$\frac{\sqrt{3}}{3}$),
若点D在AB下方,由∠BAD=∠DBA=30°,AB=2,得D2(-1,-$\frac{2\sqrt{3}}{3}$),
②当AB为腰时,A为顶点时,
∵∠DAB=120°,∠OAB=60°,AD=AB=2,
∴点D在y轴或x轴上,
若D在y轴上,得D3(0,$\sqrt{3}$),若D在x轴上,得D4(-3,0);
③当AB为腰时,A为顶点时,
若点D在第三象限,
∵∠DBO=150°,BD=2,得D5(-1,-2$\sqrt{3}$);
若点D在第四象限时,
∵DB∥x轴,BD=2,得D6(2,-$\sqrt{3}$),
∴符合要求的点D的坐标为(0,-$\frac{\sqrt{3}}{3}$),(-1,-$\frac{2\sqrt{3}}{3}$),(0,$\sqrt{3}$),(-3,0),(-1,-2$\sqrt{3}$),(2,-$\sqrt{3}$);
(3)当AP+BQ最小时,四边形ABQP的周长最小,
把点B向上平移$\frac{\sqrt{3}}{3}$个单位后得到B1(0,-$\frac{2\sqrt{3}}{3}$),
∵BB1∥PQ,且BB1=PQ,
∴四边形BB1PQ是平行四边形,
∴BQ=B1P,
∴AP+BQ=AP+B1P,
要在直线x=$\frac{1}{2}$上找一点P,使得AP+B1P最小,
作点B1关于直线x=$\frac{1}{2}$的对称点,得B2(1,-$\frac{2\sqrt{3}}{3}$),
则AB2就是AP+BQ的最小值,AB2=$\sqrt{{2}^{2}+(\frac{2\sqrt{3}}{3})^{2}}$=$\frac{4\sqrt{3}}{3}$,
AB=2,PQ=$\frac{\sqrt{3}}{3}$,
∴四边形ABQP的周长最小值是$\frac{5\sqrt{3}}{3}$+2.
点评 本题考查了二次函数综合题,涉及二次函数与x轴的交点、与y轴的交点、等腰三角形的性质、勾股定理等内容,存在性问题的出现使得难度增大.


科目:初中数学 来源: 题型:填空题
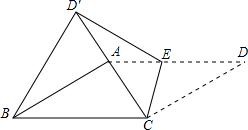 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.
如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为D′,连接D′B,若△D′BC为等边三角形,则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
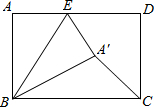 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD 的平分线上时,CA1的长为( )| A. | 3或4$\sqrt{2}$ | B. | 4或3$\sqrt{2}$ | C. | 3或4 | D. | 3$\sqrt{2}$或4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
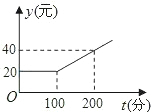 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-b+1,a+1) | B. | (-a,-b+2) | C. | (b-1,-a+1) | D. | (a,b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com