
分析 (1)利用陈老师花了300元购买甲、乙两种奖品用于奖励进步显著学生及成绩特别优秀学生,期末考试后,陈老师再次去购买奖品时,发现甲奖品每件上涨了6元,乙奖品每件上涨了12元,结果购买相同数量的甲、乙两种奖品却多花了120元,可得y与x之间的函数关系式;
(2)设甲奖品原单价为a元,乙奖品原单价为b元,则8a+6b=300,利用a<b≤30,可得a,b,即可得出结论.
解答 解:(1)由题意得:6x+12y=120,
解得:y=10-$\frac{1}{2}$x;
故答案为:y=10-$\frac{1}{2}x$.
(2)当x=8时,y=6.
设甲奖品原单价为a元,甲奖品原单价为b元,则8a+6b=300.
∴b=50-$\frac{4}{3}$a,
∵a<b≤30.
∴$\left\{\begin{array}{l}50-\frac{4}{3}a≤30\\ a<50-\frac{4}{3}a.\end{array}$,
解得15≤a<$\frac{150}{7}$.
经检验,a=18符合题意,
此时b=26.
设最多可购买z件乙奖品,
∴24×7+38z≤300,
∴z≤$\frac{66}{19}$,
∴z=3.
答:最多买3件乙奖品,才能把奖品总费用控制在300元以内.
点评 本题考查了一次函数的应用,利用数学知识解决实际问题,考查学生分析解决问题的能力,确定函数关系是关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
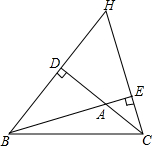 已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
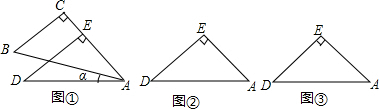
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
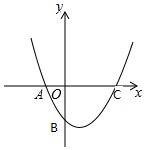 设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
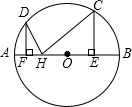 如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.
如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com