练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．下列命题中，是假命题的是（　　）
    A．互余两角的和是90°B．全等三角形的面积相等
    C．等边三角形是中心对称图形D．两直线平行，同旁内角互补

    分析 分别利用互余的性质以及等边三角形的性质和全等三角形的性质和平行线的性质分析求出即可．

    解答 解：A、互余两角的和是90°，正确，不合题意；
    B、全等三角形的面积相等，正确，不合题意；
    C、等边三角形不是中心对称图形，故错误，符合题意；
    D、两直线平行，同旁内角互补，正确，不合题意；
    故选：C．

    点评 此题主要考查了命题与定理，正确把握相关定理是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

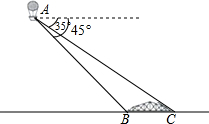    19．小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B，C两点的俯角分别为45°，35°．已知大桥BC与地面在同一水平面上，其长度为100m，请求出热气球离地面的高度．（结果保留整数）
    （参考数据：sin35°≈$\frac{7}{12}$，cos35°≈$\frac{5}{6}$，tan35°≈$\frac{7}{10}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

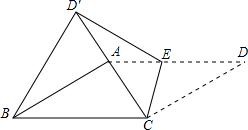    3．如图，四边形ABCD是菱形，AB=2，∠ABC=30°，点E是射线DA上一动点，把△CDE沿CE折叠，其中点D的对应点为D′，连接D′B，若△D′BC为等边三角形，则DE=2$\sqrt{3}$-2或$\sqrt{3}$+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．方程x（x+1）=5（x+1）的根是（　　）
    A．-1B．5C．1 或5D．-1或5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，用同样规格黑白两色的正方形瓷砖铺设长方形地面，请观察下列图形，并解答有关问题：

    （1）在第n个图中，第一横行共n+3 块瓷砖，第一竖列共有n+2 块瓷砖；（均用含n的代数式表示）铺设地面所用瓷砖的总块数为n2+5n+6或（n+2）（n+3）；（用含n的代数式表示，n表示第n个图形）
    （2）上述铺设方案，铺一块这样的长方形地面共用了506块瓷砖，求此时n的值；
    （3）黑瓷砖每块4元，白瓷砖每块3元，在问题（2）中，共需要花多少钱购买瓷砖？
    （4）是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．滨湖区教育局准备组织一次初中生篮球赛，赛制为单循环形式（每两队之间都赛一场），报名后经计算共需安排28场比赛．若有x所学校报名，每所学校安排一支球队参赛，则根据题意可列方程：$\frac{x（x-1）}{2}$=28．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．为了调动同学们的学习积极性，某班班主任陈老师在班级管理中采用了奖励机制，每次期中期末考试后都会进行表彰奖励．期中考试后，陈老师花了300元购买甲、乙两种奖品用于奖励进步显著学生及成绩特别优秀学生．期末考试后，陈老师再次去购买奖品时，发现甲奖品每件上涨了6元，乙奖品每件上涨了12元，结果购买相同数量的甲、乙两种奖品却多花了120元．设陈老师每次购买甲奖品x件，乙奖品y件．
    （1）请直接写出y与x之间的函数关系式：y=10-$\frac{1}{2}x$．
    （2）若x=8，且这两种奖品不再调价．若陈老师再次去购买奖品，且所买甲奖品比前两次都少1件，则他最多买几件乙奖品，才能把奖品总费用控制在300元以内？
    【备注：已知陈老师第一次购买奖品发现，甲奖品比乙奖品便宜，两种奖品单价（元）都在30以内且为偶数】

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．∠A+∠B+∠C+∠D+∠E+∠F的度数=360°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

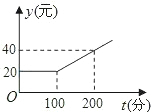    2．有甲、乙两家通迅公司，甲公司每月通话的收费标准如图所示；乙公司每月通话收费标准如表所示：
    月租费通话费
    25元0.15元/分钟
    （1）通话时间为多少时，两家公司的收费是相同的？
    （2）李女士想买一部手机，如果她的月通话时间不超过100分钟，她选择哪家通讯公司更合算？如果她的月通话时间超过100分钟，又将如何选择？

    查看答案和解析>>

    同步练习册答案