
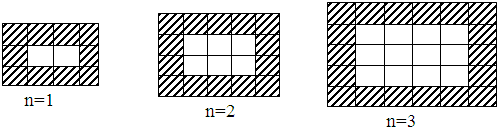
分析 (1)第一个图形用的正方形的个数=3×4=12,第二个图形用的正方形的个数=4×5=20,第三个图形用的正方形的个数=5×6=30…以此类推,第n个图形用的正方形的个数=(n+2)(n+3)个;
(2)根据题意可得(n+2)(n+3)=506,解关于n的一元二次方程即可;
(3)观察图形可知,每-横行有白砖(n+1)块,每-竖列有白砖n块,因而白砖总数是n(n+1)块;
(4)第一个图形中白色瓷块有1×2=2,黑色瓷块=2×5=10,
第二个图形中白色瓷块有2×3=6,黑色瓷块=2×7=14,
第三个图形中白色瓷块有3×4=12,黑色瓷块=2×9=18…
那么依此类推第n个图形中有白色瓷块=n(n+1),黑色瓷块=2(2n+3),根据题意可得n(n+1)=2(2n+3),解关于n的方程即可.
解答 解:如图:
(1)第一个图形用的正方形的个数=3×4=12,第二个图形用的正方形的个数=4×5=20,第三个图形用的正方形的个数=5×6=30…以此类推,第n个图形用的正方形的个数=(n+2)(n+3)个;
故答案为:n2+5n+6或(n+2)(n+3);
(2)根据题意得:n2+5n+6=506,
解得n1=20,n2=-25(不符合题意,舍去);
(3)观察图形可知,每-横行有白砖(n+1)块,每-竖列有白砖n块,因而白砖总数是n(n+1)块,n=20时,白砖为20×21=420(块),黑砖数为506-420=86(块).
故总钱数为420×3+86×4=1260+344=1604(元),
答:共花1604元钱购买瓷砖.
(4)根据题意得:n(n+1)=2(2n+3),
解得n=$\frac{3±\sqrt{33}}{2}$(不符合题意,舍去),
∴不存在黑瓷砖与白瓷砖块数相等的情形.
点评 本题考查了一元二次方程的应用,解题的关键主要是寻找规律,还使用了解一元二次方程的知识.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤3 | B. | m<3 | C. | m<3且m≠2 | D. | m≤3且m≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
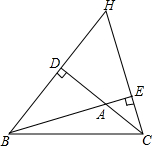 已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
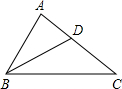 如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
如图,在△ABC中,BD平分∠ABC,∠A=2∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com