
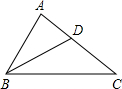
 如图,在△ABC中,BD平分∠ABC,∠A=2∠C.
如图,在△ABC中,BD平分∠ABC,∠A=2∠C.分析 (1)在BC上截取BE=AB,利用“边角边”证明△ABD和△BED全等,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,然后结合图形整理即可得证;
(2)由(1)知:△ABD≌△BED,根据全等三角形对应边相等可得DE=AD,全等三角形对应角相等可得∠AED=∠A,然后求出∠C=∠CDE,根据等角对等边可得CE=DE,等量代换得到EC=AD,即得答案BC=BE+EC=AB+AD;
(3)为了把∠A=2∠C转化成两个角相等的条件,可以构造辅助线:在AC上取BF=BA,连接AE,根据线段的垂直平分线的性质以及三角形的内角和定理的推论能够证明AB=F.再根据勾股定理表示出BC2,AB2.再运用代数中的公式进行计算就可证明.
解答 解:(1)在BC上截取BE=BA,如图1,
在△ABD和△BED中,
$\left\{\begin{array}{l}{BE=BA}\\{∠ABD=∠EBD}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△BED,
∴∠BED=∠A,
∵∠C=38°,∠A=2∠C,
∴∠A=76°,
∴∠ABC=180°-∠C-∠A=66°,
BD平分∠ABC,
∴∠ABD=33°;
(2)由(1)知:△ABD≌△BED,
∴BE=AB,DE=AD,∠BED=∠A,
又∵∠A=2∠C,
∴∠BED=∠C+∠EDC=2∠C,
∴∠EDC=∠C,
∴ED=EC,
∴EC=AD
∴BC=BE+EC=AB+AD;
(3)如图2, 过B作BG⊥AC于G,
过B作BG⊥AC于G,
以B为圆心,BA长为半径画弧,交AC于F,
则BF=BA,
在Rt△ABG和Rt△GBG中,
$\left\{\begin{array}{l}{BA=BF}\\{AG=AG}\end{array}\right.$,
∴Rt△ABG≌Rt△GBG,
∴AG=FG,
∴∠BFA=∠A,
∵∠A=2∠C,
∴∠BFA=∠FBC+∠C=2∠C,
∴∠FBC=∠C,
∴FB=FC,
FC=AB,
在Rt△ABG和Rt△BCG中,
BC2=BG2+CG2,
AB2=BG2+AG2
∴BC2-AB2=CG2-AG2=(CG+AG)(CG-AG)
=AC(CG-GF)=AC•FC
=AC•AB.
点评 本题考查了全等三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等角对等边的性质,作辅助线构造出全等三角形和等腰三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50° | B. | 100° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
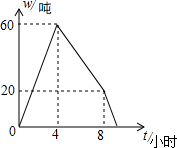 某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出物资的速度均保持不变).该仓库库存物资w(吨)与时间t(小时)之间的关系如图所示,求这批物资从开始调进到全部调出所需要的时间.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
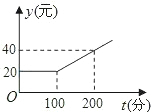 有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:
有甲、乙两家通迅公司,甲公司每月通话的收费标准如图所示;乙公司每月通话收费标准如表所示:| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
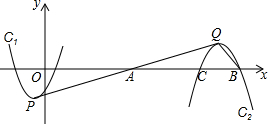 如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.
如图,抛物线C1:y=x2+2x-3的顶点为P,将该抛物线绕点A(a,0)(a>0)旋转180°后得到的抛物线C2,抛物线C2的顶点为Q,与x轴的交点是B、C,点B在点C的右侧.若∠PQB=90°,则a=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
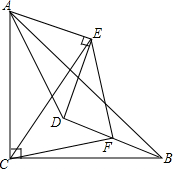 如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.
如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com