
分析 把y=2x+1和y=3x+b组成方程组,解关于x、y的方程组,求出交点坐标,根据第二象限点的坐标特征解不等式得到答案.
解答 解:由题意得,
$\left\{\begin{array}{l}{y=2x+1}\\{y=3x+b}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=1-b}\\{y=3-2b}\end{array}\right.$,
所以直线y=2x+1和y=3x+b的交点坐标为(1-b,3-2b),
∵交点在第二象限,
∴$\left\{\begin{array}{l}{1-b<0}\\{3-2b>0}\end{array}\right.$,
解得,1<b<$\frac{3}{2}$.
故答案为:1<b<$\frac{3}{2}$.
点评 本题考查的是两条直线相交的问题,正确求出交点、根据题意列出不等式组是解题的关键,注意第二象限点的横坐标小于0,纵坐标大于0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
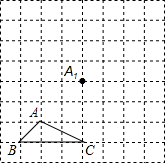 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
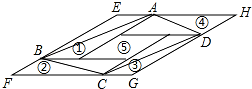 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a2-a2=2 | B. | (-a)6÷(-a)2=(-a)3 | C. | (a+b)2=a2+b2 | D. | 2a-1=$\frac{2}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com