
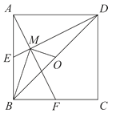
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
【答案】D
【解析】
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,从而判断①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得![]() ,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
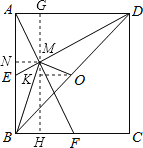
,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
MF,判断出⑤正确;过点M作MN⊥AB于N,求出MN、NB,然后利用勾股定理列式求出BM,过点M作GH∥AB,过点O作OK⊥GH于K,然后求出OK、MK,再利用勾股定理列式求出MO,根据正方形的性质求出BO,然后利用勾股定理逆定理判断出∠BMO=90°,从而判断出③正确.
在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=![]() BC,
BC,
在△ABF和△DAE中,
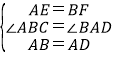 ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°-(∠ADE+∠DAF)=180°-90°=90°,
∴∠AME=180°-∠AMD=180°-90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴![]()
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=![]()
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴![]() ,
,
即![]() ,
,
解得AM=![]()
∴MF=AF-AM=![]() ,
,
∴AM=![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则
![]()
即![]()
解得MN=![]() ,AN=
,AN=![]() ,
,
∴NB=AB-AN=2a-![]() =
=![]() ,
,
根据勾股定理,BM=![]()
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a-![]() =
=![]() ,MK=
,MK=![]() -a=
-a=![]() ,
,
在Rt△MKO中,MO=![]()
根据正方形的性质,BO=2a×![]() ,
,
∵BM2+MO2=![]()
![]()
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选:D


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
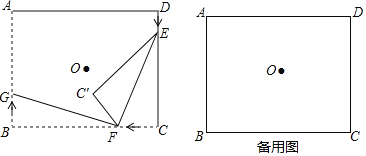
【题目】如图,点O为矩形ABCD对角线交点,![]() ,
,![]() ,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为
,点E、F、G分别从D,C,B三点同时出发,沿矩形的边DC、CB、BA匀速运动,点E的运动速度为![]() ,点F的运动速度为
,点F的运动速度为![]() ,点G的运动速度为
,点G的运动速度为![]() ,当点F到达点
,当点F到达点![]() 点F与点B重合
点F与点B重合![]() 时,三个点随之停止运动
时,三个点随之停止运动![]() 在运动过程中,
在运动过程中,![]() 关于直线EF的对称图形是
关于直线EF的对称图形是![]() 设点E、F、G运动的时间为
设点E、F、G运动的时间为![]() 单位:
单位:![]()
![]() 当
当![]() ______s时,四边形
______s时,四边形![]() 为正方形;
为正方形;
![]() 若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
若以点E、C、F为顶点的三角形与以点F、B、G为顶点的三角形相似,求t的值;
![]() 是否存在实数t,使得点
是否存在实数t,使得点![]() 与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
与点O重合?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
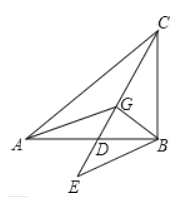
【题目】如图,点G是△ABC的重心,CG的延长线交AB于D,GA=5,GC=4,GB=3,将△ADG绕点D顺时针方向旋转180°得到△BDE,则△EBC的面积=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
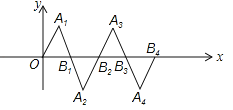
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A. (4n﹣1,![]() )B. (2n﹣1,
)B. (2n﹣1,![]() )C. (4n+1,
)C. (4n+1,![]() )D. (2n+1,
)D. (2n+1,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
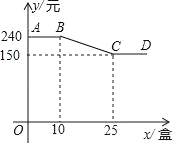
【题目】中秋节前夕,某公司的李会计受公司委派去超市购买若干盒美心月饼,超市给出了该种月饼不同购买数量的价格优惠,如图,折线ABCD表示购买这种月饼每盒的价格y(元)与盒数x(盒)之间的函数关系.
(1)当购买这种月饼盒数不超过10盒时,一盒月饼的价格为 元;
(2)求出当10<x<25时,y与x之间的函数关系式;
(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼?
查看答案和解析>>
科目:初中数学 来源: 题型:
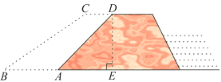
【题目】为做好汉江防汛工作,防汛指挥部决定对一段长为2500m重点堤段利用沙石和土进行加固加宽.专家提供的方案是:使背水坡的坡度由原来的1:1变为1:1.5,如图,若CD∥BA,CD=4米,铅直高DE=8米.
(1)求加固加宽这一重点堤段需沙石和土方数是多少?
(2)某运输队承包这项沙石和土的运送工程,根据施工方计划在一定时间内完成,按计划工作5天后,增加了设备,工效提高到原来的1.5倍,结果提前了5天完成任务,问按原计划每天需运送沙石和土多少m3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且c>b>a,若Rt△ABC是奇异三角形,求a:b:c;
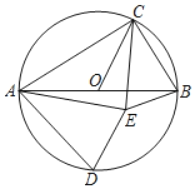
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形:
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,BE⊥AD于点E,BF⊥CD于点F,AC与BE、BF分别交于点G,H。
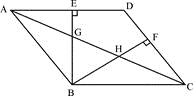
(1)求证:△BAE∽△BCF
(2)若BG=BH,求证四边形ABCD是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
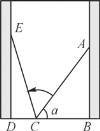
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com