
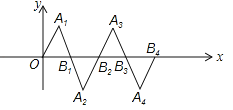
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是( )
A. (4n﹣1,![]() )B. (2n﹣1,
)B. (2n﹣1,![]() )C. (4n+1,
)C. (4n+1,![]() )D. (2n+1,
)D. (2n+1,![]() )
)
【答案】C
【解析】
试题∵△OA1B1是边长为2的等边三角形,∴A1的坐标为(1,![]() ),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0﹣
),B1的坐标为(2,0),∵△B2A2B1与△OA1B1关于点B1成中心对称,∴点A2与点A1关于点B1成中心对称,∵2×2﹣1=3,2×0﹣![]() =﹣
=﹣![]() ,∴点A2的坐标是(3,﹣
,∴点A2的坐标是(3,﹣![]() ),∵△B2A3B3与△B2A2B1关于点B2成中心对称,∴点A3与点A2关于点B2成中心对称,∵2×4﹣3=5,2×0﹣(﹣
),∵△B2A3B3与△B2A2B1关于点B2成中心对称,∴点A3与点A2关于点B2成中心对称,∵2×4﹣3=5,2×0﹣(﹣![]() )=
)=![]() ,∴点A3的坐标是(5,
,∴点A3的坐标是(5,![]() ),∵△B3A4B4与△B3A3B2关于点B3成中心对称,∴点A4与点A3关于点B3成中心对称,∵2×6﹣5=7,2×0﹣
),∵△B3A4B4与△B3A3B2关于点B3成中心对称,∴点A4与点A3关于点B3成中心对称,∵2×6﹣5=7,2×0﹣![]() =﹣
=﹣![]() ,∴点A4的坐标是(7,﹣
,∴点A4的坐标是(7,﹣![]() ),…,∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,∵当n为奇数时,An的纵坐标是
),…,∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是﹣
,当n为偶数时,An的纵坐标是﹣![]() ,∴顶点A2n+1的纵坐标是
,∴顶点A2n+1的纵坐标是![]() ,∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,
,∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).故选:C.
).故选:C.


科目:初中数学 来源: 题型:
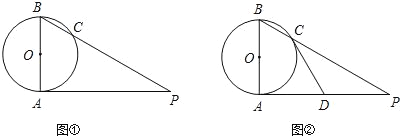
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若∠P=35°,求∠ABP的度数;
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
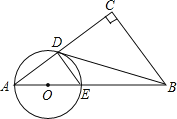
【题目】已知:在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
(1)观察图形,猜想BD与⊙O的位置关系;
(2)证明第(1)题的猜想
查看答案和解析>>
科目:初中数学 来源: 题型:
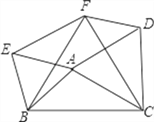
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF。
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足_____________________时,四边形AEFD是菱形。(无需证明)
②△ABC满足_______________________时,四边形AEFD是矩形。(无需证明)
③△ABC满足_______________________时,四边形AEFD是正方形。(无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
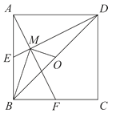
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
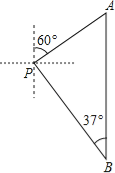
【题目】小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P处观看小亮与爸爸在湖中划船(如图所示).小船从P处出发,沿北偏东60°方向划行200米到A处,接着向正南方向划行一段时间到B处.在B处小亮观测到妈妈所在的P处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com