
 ̉ÑÖªyÊǹØÓÚxµÄº¯Êư£¬Ç̉x£¬yÂú×ă·½³̀×é$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$
̉ÑÖªyÊǹØÓÚxµÄº¯Êư£¬Ç̉x£¬yÂú×ă·½³̀×é$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$·ÖÎö £¨1£©ÓÉ$\left\{\begin{array}{l}{x=3y=4-a}&{¢Ù}\\{x-y=3a}&{¢Ú}\end{array}\right.$£¬¢Ù¡Á3+¢ÚµĂµ½£¬4x+8y=12£¬¼´y=-$\frac{1}{2}$x+$\frac{3}{2}$£¬»³ö̉»´Îº¯ÊưµÄͼÏó¼´¿É£®
£¨2£©ÓÉ¡÷BCDÓë¡÷ABCÏàËÆ£¨²»°üÀ¨È«µÈ£©£¬ÍƳö¡ÏABD=90¡ă£¬ÓÉ¡÷BCD¡×¡÷ACB£¬ÍƳö$\frac{BC}{CA}$=$\frac{DC}{BC}$£¬Çó³öCD¿ÉµĂD£¨-2£¬0£©£¬ÔÙ¸ù¾Ư¶Ô³ÆÖá¿ÉµĂD¡ä×ø±ê£¨1£¬0£©̉²Âú×ằơ¼₫£®
£¨3£©Èçͼ3ÖĐ£¬µ±¡ÑPÓëÖ±ÏßABÏàÇĐʱ£¬ÉèÇеăΪE£¬Á¬½ÓPE£¬ÓÉsin¡ÏBAC=$\frac{BC}{AB}$=$\frac{PE}{AP}$£¬¿ÉµĂ$\frac{2}{2\sqrt{5}}$=$\frac{1}{AP}$£¬ÍƳöAP=$\sqrt{5}$£¬ÍƳöOP=3-$\sqrt{5}$£¬´Ëʱm=3-$\sqrt{5}$£¬µ±¡ÑPÓëÖ±ÏßABÏàÇĐÓÚµăFʱ£¬Í¬·¨¿ÉµĂAP¡ä=$\sqrt{5}$£¬´Ëʱm=3+$\sqrt{5}$£¬Óɴ˼´¿É½â¾öÎỀ⣮
£¨4£©ƠâÑùµÄm´æÔÚ£®µ±d£¨-2£¬0£©Ê±£¬·ÖÁ½ÖÖÇéĐÎ̀ÖÂÛ¢Ùµ±MN¡ÎBDʱ£¬¡÷AMN¡×¡÷ABD£®¢Úµ±MN¡ÍADʱ£¬¡÷AMN¡×¡÷ADB£®·Ö±đÁĐ·½³̀¼´¿É½â¾öÎỀ⣻µ±D£¨-1£¬0£©Ê±Í¬·¨¿ÉÇó£®
½â´đ ½â£º£¨1£©ÓÉ$\left\{\begin{array}{l}{x=3y=4-a}&{¢Ù}\\{x-y=3a}&{¢Ú}\end{array}\right.$£¬
¢Ù¡Á3+¢ÚµĂµ½£¬4x+8y=12£¬
¡ày=-$\frac{1}{2}$x+$\frac{3}{2}$£®
º¯ÊưͼÏóÈçͼ1Ëùʾ£®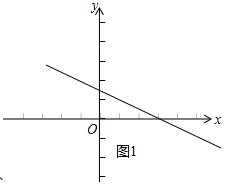
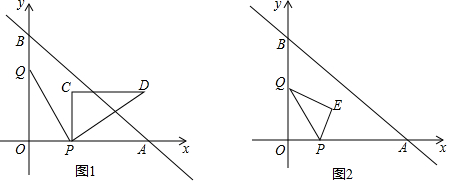
£¨2£©Èçͼ2ÖĐ£¬
¡ß¡÷BCDÓë¡÷ABCÏàËÆ£¨²»°üÀ¨È«µÈ£©£¬
¡à¡ÏABD=90¡ă£¬
¡ßC£¨-1£¬0£©£¬B£¨-1£¬2£©£¬A£¨3£¬0£©£¬
BC=2£¬AC=4£¬
¡ß¡ÏDBC+¡ÏBDC=90¡ă£¬¡ÏBDC+¡ÏBAC=90¡ă£¬
¡à¡ÏDBC=¡ÏBAC£¬¡ß¡ÏBCD=¡ÏBCA£¬
¡à¡÷BCD¡×¡÷ACB£¬
¡à$\frac{BC}{CA}$=$\frac{DC}{BC}$£¬
¡à$\frac{2}{4}$=$\frac{DC}{2}$£¬
¡àCD=1£¬
¡àD£¨-2£¬0£©£®
¸ù¾Ư¶Ô³ÆĐÔµ±D¡ä£¨1£¬0£©Ê±£¬¡÷BCD¡äÓë¡÷ABCÏàËÆ£¬
×ÛÉÏËùÊö£¬µ±µăD×ø±êΪ£¨-2£¬0£©»̣£¨1£¬0£©Ê±£¬¡÷BCDÓë¡÷ABCÏàËÆ£¨²»°üÀ¨È«µÈ£©£®
£¨3£©Èçͼ3ÖĐ£¬
µ±¡ÑPÓëÖ±ÏßABÏàÇĐʱ£¬ÉèÇеăΪE£¬Á¬½ÓPE£¬
ÔÚRt¡÷APEÖĐ£¬¡ß¡ÏAEP=90¡ă£¬PE=1£¬
ÓÉsin¡ÏBAC=$\frac{BC}{AB}$=$\frac{PE}{AP}$£¬
¡à$\frac{2}{2\sqrt{5}}$=$\frac{1}{AP}$£¬
¡àAP=$\sqrt{5}$£¬
¡àOP=3-$\sqrt{5}$£¬´Ëʱm=3-$\sqrt{5}$£¬
µ±¡ÑPÓëÖ±ÏßABÏàÇĐÓÚµăFʱ£¬Í¬·¨¿ÉµĂAP¡ä=$\sqrt{5}$£¬´Ëʱm=3+$\sqrt{5}$£¬
¡à̉ÔPΪԲĐÄ£¬1Ϊ°ë¾¶µÄÔ²Ó루1£©º¯ÊưµÄͼÏóÓĐ½»µăʱ£¬mµÄÈ¡Öµ·¶Î§Îª3-$\sqrt{5}$¡Üm¡Ü3+$\sqrt{5}$£®
£¨4£©ƠâÑùµÄm´æÔÚ£®Èçͼ4ÖĐ£¬
ÔÚRt¡÷ABCÖĐ£¬Óɹ´¹É¶¨ÀíµĂAB=2$\sqrt{5}$£¬
µ±MN¡ÎBDʱ£¬¡÷AMN¡×¡÷ABD£¬Ộ$\frac{AM}{AB}$=$\frac{AN}{AD}$£¬
¡à$\frac{n}{2\sqrt{5}}$=$\frac{5-n}{5}$£¬
½âµĂn=10$\sqrt{5}$-20£¬
Èçͼ5ÖĐ£¬
µ±MN¡ÍADʱ£¬¡÷AMN¡×¡÷ADB£¬
Ộ $\frac{AM}{AD}$=$\frac{AN}{AB}$£¬
¡à$\frac{n}{5}$=$\frac{5-n}{2\sqrt{5}}$£¬
½âµĂn=25-10$\sqrt{5}$£¬
µ±D£¨1£¬0£©Ê±£¬Í¬·¨¿ÉµĂnµÄֵΪ$\frac{5-\sqrt{5}}{2}$»̣$\frac{\sqrt{5}-1}{2}$£¬
×ÛÉÏËùÊö£¬Âú×ằơ¼₫µÄnµÄֵΪ10$\sqrt{5}$-20»̣25-10$\sqrt{5}$»̣$\frac{5-\sqrt{5}}{2}$»̣$\frac{\sqrt{5}-1}{2}$£®
µăÆÀ ±¾̀⿼²éÏàËÆÈư½ÇĐεÄÅж¨ºÍĐÔÖÊ¡¢Ô²ÓëÖ±ÏßµÄλÖĂ¹Øϵ¡¢¶₫Ôª̉»´Î·½³̀×é¡¢¹´¹É¶¨Àí¡¢Æ½ĐĐÏßµÄĐÔÖʵÈ֪ʶ£¬½ầâµÄ¹Ø¼üÊÇÁé»îÔËÓĂËùѧ֪ʶ½â¾öÎỀ⣬ѧ»áÀûÓĂͼĐεÄ̀ØÊâλÖĂ½â¾öÎỀ⣬ѧ»áÓĂ·ÖÀà̀ÖÂÛµÄ˼Ïë˼¿¼ÎỀ⣬ÊôÓÚÖĐ¿¼Ñ¹Öá̀⣮



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | Èôa£¾0£¬b£¼0£¬Ộ$\frac{b}{a}$£¾0 | B£® | Èôa£¼0£¬b£¼0£¬Ộab£¼0 | ||
| C£® | Èôa£¾b£¬Ộa-b£¾0 | D£® | Èôa£¾b£¬a£¼0£¬Ộ$\frac{b}{a}$£¼0 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
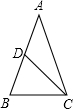 ̉ÑÖªµÈÑüÈư½ÇĐΡ÷ABC£¬AB=AC£¬̉»ÑüÉϵÄÖĐÏß°ÑƠâ¸öÈư½ÇĐεÄÖܳ¤·Ö³É12ºÍ15Á½²¿·Ö£¬ÇóƠâ¸öÈư½ÇĐεÄÈư±ß³¤£®
̉ÑÖªµÈÑüÈư½ÇĐΡ÷ABC£¬AB=AC£¬̉»ÑüÉϵÄÖĐÏß°ÑƠâ¸öÈư½ÇĐεÄÖܳ¤·Ö³É12ºÍ15Á½²¿·Ö£¬ÇóƠâ¸öÈư½ÇĐεÄÈư±ß³¤£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | a3•a2=a6 | B£® | £¨¦Đ-3.14£©0=1 | C£® | £¨$\frac{1}{2}$£©-1=-2 | D£® | $\sqrt{9}$=¡À3 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
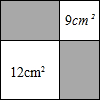 Èçͼ£¬´Ó̉»¸öƠư·½ĐÎÖĐ½ØÈ¡Ăæ»ưΪ9cm2»̣12cm2µÄÁ½¸öĐ¡Ơư·½ĐΣ¬ỘÁôÏẨơÓ°²¿·ÖµÄĂæ»ưΪ12$\sqrt{3}$cm2£®
Èçͼ£¬´Ó̉»¸öƠư·½ĐÎÖĐ½ØÈ¡Ăæ»ưΪ9cm2»̣12cm2µÄÁ½¸öĐ¡Ơư·½ĐΣ¬ỘÁôÏẨơÓ°²¿·ÖµÄĂæ»ưΪ12$\sqrt{3}$cm2£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com