
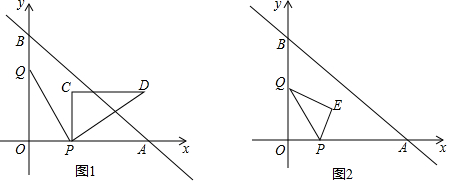
���� ��1�����OQ��OP�ij����ɽ�����⣮
��2����ͼ1�У���PQ��ABʱ���ı���PQBA�����Σ��ɵ�$\frac{OQ}{OB}$=$\frac{OP}{OA}$����$\frac{6-3t}{6}$=$\frac{4t}{8}$���ⷽ�̼��ɣ�
��3����t��ʾ��D���꣬����ֱ�ߵĽ���ʽ���ɽ�����⣮
��4�����������ηֱ��г����̼��ɽ�����⣮
��� �⣺��1��������BQ=3t��OP=4t��
����ֱ��y=-$\frac{3}{4}$x+6����x=0��y=6����y=0��x=8��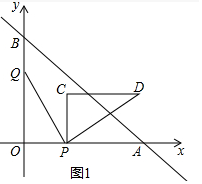
��B��0��6����A��8��0����
��OB=6��OA=8��
��Q��0��6-3t����P��4t��0����
��2����ͼ1�У���PQ��ABʱ���ı���PQBA�����Σ�
��$\frac{OQ}{OB}$=$\frac{OP}{OA}$��
��$\frac{6-3t}{6}$=$\frac{4t}{8}$��
��t=1��
��t=1sʱ���ı���PQBA�����Σ�
��3��������D��4t+6-3t��4t������D��t+6��4t����
�ߵ�D��ֱ��y=-$\frac{3}{4}$x+6�ϣ�
��4t=-$\frac{3}{4}$��t+6��+6��
��t=$\frac{6}{19}$s��
��t=$\frac{6}{19}$sʱ������D����ֱ��AB��ʱ��
��4����ͼ2�У�
�ٵ�PQ��ABʱ���ɣ�2����֪t=1s��
�ڵ�EQ��OAʱ��PE=OP=OQ����6-3t=4t����t=$\frac{6}{7}$s��
�۵�PE��OBʱ����OQP=��QPO=��QPE=45�㣬
��OQ=OP��
��6-3t=4t��
��t=$\frac{6}{7}$s��
�ܵ�QE��ABʱ����ͼ3�У��ӳ�QE��OA��F��
�ɡ�PEF�ס�BOA��$\frac{PE}{OB}$=$\frac{PF}{AB}$��
��PF=$\frac{20t}{3}$��
��OF=$\frac{32t}{3}$��
��$\frac{OQ}{OB}$=$\frac{OF}{OA}$��
��$\frac{6-3t}{6}$=$\frac{\frac{32}{3}t}{8}$��
��t=$\frac{6}{11}$s��
�ݵ�PE��AB����ͼ4�У��ӳ�PE��OB��F��
�ɡ�QEF�ס�ABO���õ�$\frac{QF}{AB}$=$\frac{QE}{OA}$���ɵ�QF=$\frac{5}{4}$��6-3t����
��OF=$\frac{9}{4}$��6-3t����
��$\frac{OF}{OB}$=$\frac{OP}{OA}$��
��$\frac{\frac{9}{4}��6-3t��}{6}$=$\frac{4t}{8}$��
��t=$\frac{18}{13}$��
��������������PEQ��һ����ABƽ��ʱ��t��ֵΪ1s��$\frac{6}{7}$s��$\frac{6}{11}$s��$\frac{18}{13}$s��
���� ���⿼��һ�κ����ۺ��⡢ƽ���߷��߶γɱ������������������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣮�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڳ������У�����AA��ƽ�е�ֱ����DD�䣬BB�䣬CC�䣬����AA��ƽ�е�����BCC��B����CC��D��D��
��ͼ��ʾ���ڳ������У�����AA��ƽ�е�ֱ����DD�䣬BB�䣬CC�䣬����AA��ƽ�е�����BCC��B����CC��D��D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪y�ǹ���x�ĺ�������x��y���㷽����$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$
��֪y�ǹ���x�ĺ�������x��y���㷽����$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | -2 | C�� | 0 | D�� | -$\frac{5}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
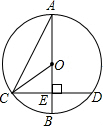 ��ͼ���ڡ�O�У�ֱ��AB����CD��ֱ�ཻ�ڵ�E������AC��OC������A=30�㣬OC=4������CD�ij��ǣ�������
��ͼ���ڡ�O�У�ֱ��AB����CD��ֱ�ཻ�ڵ�E������AC��OC������A=30�㣬OC=4������CD�ij��ǣ�������| A�� | $2\sqrt{3}$ | B�� | 4 | C�� | $4\sqrt{3}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com