
【题目】一次函数![]() 与一次函数
与一次函数![]() 的图象的交点的纵坐标为
的图象的交点的纵坐标为![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)1;(2)证明见解析.
【解析】
(1)联立一次函数解析式,根据交点纵坐标为![]() ,可一求得交点横坐标为1,进而得到a +b +c =2,对所给式子
,可一求得交点横坐标为1,进而得到a +b +c =2,对所给式子![]() 进行化简,将a +b +c =2代入即可求出
进行化简,将a +b +c =2代入即可求出![]() 的值;
的值;
(2)a + b + c =2,平方化简得a2 + b2 + c2 = 4-2×1 = 2,对所求证的式子进行变形得,(b-a)[1-2(a + b) + (b2 + a2 + ab)] = 0,分类进行讨论即可.
(1)依题意得:![]() ,且abc≠0,
,且abc≠0,
由①得:x=1,代入②得:a + b + c =2
![]()
a3 + b3 + c3-3abc-2(a2 + b2 + c2) + (a + b + c) = 0
(a + b + c)(a2 + b2 + c2-ab-bc-ca)-2(a2 + b2 + c2) + (a + b + c) = 0
2(a2 + b2 + c2-ab-bc-ca)-2(a2 + b2 + c2) + 2 = 0
ab + bc + ca = 1
(2)(a + b + c)2 = 22 = a2 + b2 + c2 + 2(ab + bc + ca)
a2 + b2 + c2 = 4-2×1 = 2
当![]() 时,要证:
时,要证:![]() ,
,
只需证:b(1-b)2 = a(1-a)2
b(1-b)2-a(1-a)2 = 0
b-a-2(b2-a2) + (b3-a3) = 0
(b-a)[1-2(a + b) + (b2 + a2 + ab)] = 0 (*)
i)当a = b时,(*)式显然成立;
ii)当a≠b时,
∵ a + b + c = 2,a2 + b2 + c2 = 2,ab + bc + ca = 1
∴ a + b = 2-c,a2 + b2 = 2-c2,ab = 1-c(a + b) = 1-c(2-c)
∴ 1-2(a + b) + (b2 + a2 + ab) = 1-2(2-c) + 2-c2 + 1-c(2-c)
= 1-4+2c+2-c2+1-2c+c2
= 0
∴ (*)式成立.
综上,当![]() 时,均有
时,均有![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: ![]()
B.1: ![]()
C.1:2
D.2:3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 , 点A1的对应点为点A2 . 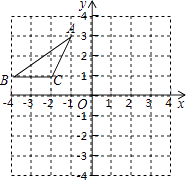
(1)画出△A1B1C1;
(2)画出△A2B2C2;
(3)求出在这两次变换过程中,点A经过点A1到达A2的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D在边AB的延长线上,BD=3,过点D作DE⊥AB,与边AC的延长线相交于点E,以DE为直径作⊙O交AE于点F. 
(1)求⊙O的半径及圆心O到弦EF的距离;
(2)连接CD,交⊙O于点G(如图2).求证:点G是CD的中点. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.
(1)根据下表提供的数据,求y与x的函数关系式;当水价为每吨10元时,1吨水生产出的饮料所获的利润是多少?
1吨水价格x(元) | 4 | 6 |
用1吨水生产的饮料所获利润y(元) | 200 | 198 |
(2)为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费.已知该厂日用水量不少于20吨,设该厂日用水量为t吨,当日所获利润为W元,求W与t的函数关系式;该厂加强管理,积极节水,使日用水量不超过25吨,但仍不少于20吨,求该厂的日利润的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,AC=2cm,将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置,则线段AB扫过区域(图中的阴影部分)的面积为cm2 . 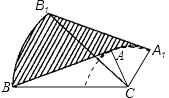
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com