
【题目】
(1)解方程: ![]()
(2)解不等式组: ![]() .
.
【答案】
(1)解:去分母得:2x﹣1+x+2=0,
解得:x=﹣ ![]() ,
,
经检验,x=﹣ ![]() 是分式方程的解;
是分式方程的解;
(2)解: ![]() ,
,
由①得:x≥1,由②得:x>3,
则不等式组的解集为x>3.
【解析】(1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出解集.
【考点精析】本题主要考查了去分母法和一元一次不等式组的解法的相关知识点,需要掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】下表是某校合唱团成员的年龄分布
年龄/岁 | 13 | 14 | 15 | 16 |
频数 | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.众数、中位数
C.平均数、方差
D.中位数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系. 
时段 | x | 还车数 | 借车数 | 存量y |
6:00﹣7:00 | 1 | 45 | 5 | 100 |
7:00﹣8:00 | 2 | 43 | 11 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= , 解释m的实际意义:;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣8交y轴于点A,交x轴正半轴于点B.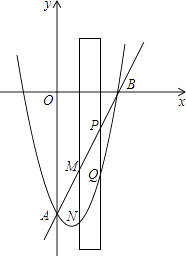
(1)求直线AB对应的函数关系式;
(2)有一宽度为1的直尺平行于y轴,在点A、B之间平行移动,直尺两长边所在直线被直线AB和抛物线截得两线段MN、PQ,设M点的横坐标为m,且0<m<3.试比较线段MN与PQ的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( ) 
A.3:4
B.![]() :2
:2 ![]()
C.![]() :2
:2 ![]()
D.2 ![]() :
: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com