
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长为__________.
的长为__________.

【答案】8或![]()
【解析】
分两种情况讨论:①当∠EFC=90°时,可知点F在对角线AC上,利用勾股定理求出AC,结合AF=AB=5可得答案;②当∠FEC=90°时,易得四边形ABEF是正方形,求出CE,利用勾股定理计算即可.
解:当△CEF为直角三角形时,有两种情况:
①当∠EFC=90°时,如图1所示,连结AC,
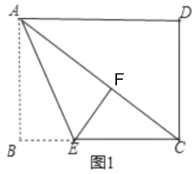
∵△ABE沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
∴点F在对角线AC上,
在Rt△ABC中,AB=5,BC=AD=12,
∴AC=![]() =13,
=13,
由折叠可得:AF=AB=5,
∴CF=13-5=8;
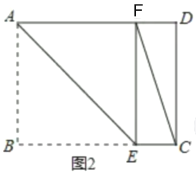
②当∠FEC=90°时,如图2所示,点F在AD上,
易得四边形ABEF是正方形,
∴AB=BE=EF=5,
∴EC=12-5=7,
∴CF=![]() ,
,
综上所述,CF的长为8或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点M为抛物线![]() 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=∠ACB,BD、CD、BE分别平分△ABC的内角∠ABC、外角∠ACP、外角∠MBC,以下结论:①AD∥BC;②DB⊥BE;③∠BDC+∠ABC=90°;④∠A+2∠BEC=180°.其中正确的结论有_____.(填序号)
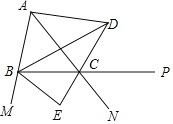
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为15万元/辆,经销一段时间后发现:当该型号汽车售价定为25万元/辆时,平均每周售出8辆;售价每降低0.5万元,平均每周多售出1辆.
(1)当售价为22万元/辆时,求平均每周的销售利润.
(2)若该店计划平均每周的销售利润是90万元,为了尽快减少库存,求每辆汽车的售价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示△ABC,AB=AC,AD⊥BC,点E、F分别是AB、AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若四边形AEDF的周长为12,两条对角线的和等于7,四边形AEDF的面积记为S1,三 角形ABC的面积记为S2,S1与S2有何数量关系_____.(直接填答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数y=![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
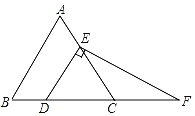
(1)求∠F的度数;
(2)若CD=4,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com