
【题目】如图所示△ABC,AB=AC,AD⊥BC,点E、F分别是AB、AC的中点.

(1)求证:四边形AEDF是菱形;
(2)若四边形AEDF的周长为12,两条对角线的和等于7,四边形AEDF的面积记为S1,三 角形ABC的面积记为S2,S1与S2有何数量关系_____.(直接填答案)
【答案】(1)详见解析;(2)2S1=S2.
【解析】
(1)根据直角三角形斜边上中线的性质,得出DE=![]() AB=AE,DF=
AB=AE,DF=![]() AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;(2)利用三角形的中线把三角形分成面积相等的两部分即可解答.
AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;(2)利用三角形的中线把三角形分成面积相等的两部分即可解答.
(1)证明:∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=![]() AB=AE,
AB=AE,
Rt△ACD中,DF=![]() AC=AF,
AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形;
(2)2S1=S2
∵点E、F分别是AB、AC的中点,
∴![]() ,
,
∴![]() ,
,
即2S1=S2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】边长相等的下列两种正多边形的组合,不能作平面镶嵌的是( )
A.正方形与正三角形B.正五边形与正三角形
C.正六边形与正三角形D.正八边形与正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s。
⑴连接AQ、CP交于点M,在点P、Q运动的过程中,∠CMQ的大小变化吗?若变化,则说明理由,若不变,请直接写出它的度数;
⑵点P、Q在运动过程中,设运动时间为t,当t为何值时,△PBQ为直角三角形?
⑶如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ的大小变化吗?则说明理由;若不变,请求出它的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或列方程组解应用题.
老京张铁路是1909年由“中国铁路之父”詹天佑主持设计建造的中国第一条干线铁路,全长约210千米,用“人”字形铁轨铺筑的方式解决了火车上山的问题.京张高铁是2022年北京至张家口冬奥会的重点配套交通基础设施,全长约175千米,预计2019年底建成通车.京张高铁的预设平均速度将是老京张铁路的5倍,可以提前5个小时到达,求京张高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2,2,3,4四个数中随机取两个数,第一个作为个位上的数字,第二个作为十位上的数字,组成一个两位数,则这个两位数是2的倍数的概率是 ( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,点E在AB上,把△ABC沿CE折叠后,点B恰好与斜边AC的中点D重合.
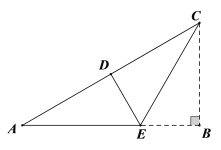
(1)求证:△ACE为等腰三角形;
(2)若AB=6,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB:![]() 分别于x,y轴交于A,B两点,过点B的直线交x轴正半轴于点C,且OB:OC=3:1.
分别于x,y轴交于A,B两点,过点B的直线交x轴正半轴于点C,且OB:OC=3:1.
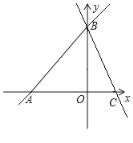
(1)直接写出点A、B、C的坐标;
(2)在线段OB上存在点P,使点P到B,C的距离相等,求出点P的坐标;
(3)在x轴上方存在点D,使得以点A,B,D为顶点的三角形与△ABC全等,求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 表示不大于x的最大整数,例如
表示不大于x的最大整数,例如![]() ,
,![]() ,
,![]() .
.
(1)将![]() 、
、![]() 、
、![]() 按照从小到大的顺序用不等号连接:_______________;
按照从小到大的顺序用不等号连接:_______________;
(2)利用(1)中的结论,方程![]() 的解为___________________.
的解为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com