【题目】边长相等的下列两种正多边形的组合，不能作平面镶嵌的是（ ）
A.正方形与正三角形B.正五边形与正三角形
C.正六边形与正三角形D.正八边形与正方形
【答案】B
【解析】
分别求出各个正多边形每个内角的度数，再结合镶嵌的条件即可作出判断．
解：A.正三角形的每个内角是60°，正方形的每个内角是90°，∵3×60°+2×90°=360°，能作平面镶嵌．
B.正三角形的每个内角是60°，正五边形每个内角是180°-360°÷5=108°，60m+108n=360°，m=6-
n，显然n取任何正整数时，m不能得正整数，故不能作平面镶嵌．
C.正三角形的每个内角是60°，正六边形的每个内角是120°，∵2×60°+2×120°=360°，能作平面镶嵌．
D.正八边形的每个内角是135°，正方形的每个内角是90°，∵2×135°+90°=360°，能作平面镶嵌．
故选：B．
53天天练系列答案科目：初中数学 来源： 题型：
【题目】问题探究：
（1）如图①所示是一个半径为
，高为4的圆柱体和它的侧面展开图，AB是圆柱的一条母线，一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点，求蚂蚁爬行的最短路程．（探究思路：将圆柱的侧面沿母线AB剪开，它的侧面展开图如图①中的矩形
则蚂蚁爬行的最短路程即为线段
的长）
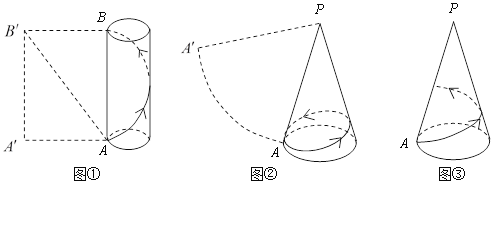
（2）如图②所示是一个底面半径为
，母线长为4的圆锥和它的侧面展开图，PA是它的一条母线，一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点，求蚂蚁爬行的最短路程．
（3）如图③所示，在②的条件下，一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点，求蚂蚁爬行的最短路程．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数
图象
轴上方的部分沿轴翻折到轴下方，图象的其余部分保持不变，翻折后的图象与原图象轴下方的部分组成一个“
”形状的新图象，若直线
与该新图象有两个公共点，则
的取值范围为_____.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点M为抛物线
与x轴的焦点为A（-3,0），B（1,0），与y轴交于点C，连结AM，AC，点D为线段AM上一动点（不与A重合），以CD为斜边在CD上侧作等腰Rt△DEC，连结AE，OE.
（1）求抛物线的解析式及顶点M的坐标；
（2）求解AD:OE的值；
（3）当△OEC为直角三角形时，求AD的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在正方形网格上有6个三角形：①△ABC；②△BCD；③△BDE；④△BFG；⑤△FGH；⑥△EFK.其中②～⑥中与①相似的是( )
A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2017年5月，某县突降暴雨，造成山体滑坡，桥梁垮塌，房屋大面积受损，该省民政厅急需将一批帐篷送往灾区．现有甲、乙两种货车，已知甲种货车比乙种货车每辆车多装20件帐篷，且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等．
(1)求甲、乙两种货车每辆车可装多少件帐篷；
(2)如果这批帐篷有1 490件，用甲、乙两种汽车共16辆装运，甲种车辆刚好装满，乙种车辆最后一辆只装了50件，其余装满，求甲、乙两种货车各有多少辆．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90°，AE=CF=5，BE=DF=12，则EF的长是（ ）
A. 7 B. 8 C. 7
D. 7
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示△ABC，AB=AC，AD⊥BC，点E、F分别是AB、AC的中点．
（1）求证：四边形AEDF是菱形；
（2）若四边形AEDF的周长为12，两条对角线的和等于7，四边形AEDF的面积记为S1，三 角形ABC的面积记为S2，S1与S2有何数量关系_____．（直接填答案）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
