
【题目】甲、乙两车从![]() 城出发匀速行驶至
城出发匀速行驶至![]() 城在个行驶过程中甲乙两车离开
城在个行驶过程中甲乙两车离开![]() 城的距离
城的距离![]() (单位:千米)与甲车行驶的时间
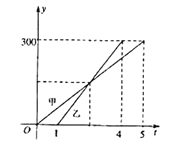
(单位:千米)与甲车行驶的时间![]() (单位:小时)之间的函数关系如图所示.则下列结论: ①
(单位:小时)之间的函数关系如图所示.则下列结论: ①![]() 两城相距
两城相距![]() 千米;②乙车比甲车晚出发
千米;②乙车比甲车晚出发![]() 小时,却早到
小时,却早到![]() 小时;③乙车出发后
小时;③乙车出发后![]() 小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距
小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距![]() 千米时,
千米时,![]() 或
或![]() ,其中正确的结论是_________.
,其中正确的结论是_________.
【答案】①②
【解析】
观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,进而得出答案.
由图象可知,A.B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
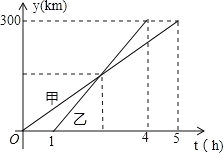
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得,k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得
![]()
解得![]()
∴y乙=100t100,
令y甲=y乙可得:60t=100t100,
解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲y乙|=50,可得|60t100t+100|=50,即|10040t|=50,
当10040t=50时,可解得t=![]() ,
,
当10040t=50时,可解得t=![]() ,
,
又当t=![]() 时,y甲=50,此时乙还没出发,
时,y甲=50,此时乙还没出发,
当t=![]() 时,乙到达B城,y甲=250;
时,乙到达B城,y甲=250;
综上可知当t的值为![]() 或
或![]() 或
或![]() 或t=
或t=![]() 时,两车相距50千米,
时,两车相距50千米,
∴④不正确;
综上,正确的有①②,
故答案为:①②


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
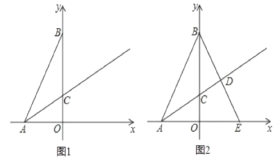
【题目】如图,平面直角坐标系中,点A(6![]() ,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.
,0),点B(0,18),∠BAO=60°,射线AC平分∠BAO交y轴正半轴于点C.
(1)求点C的坐标;
(2)点N从点A以每秒2个单位的速度沿线段AC向终点C运动,过点N作x轴的垂线,分别交线段AB于点M,交线段AO于点P,设线段MP的长度为d,点P的运动时间为t,请求出d与t的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,将△ABO沿y轴翻折,点A落在x轴正半轴上的点E,线段BE交射线AC于点D,点Q为线段OB上的动点,当△AMN与△OQD全等时,求出t值并直接写出此时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为灾区开展了“献出我们的爱”赈灾捐款活动,九年级(1)班50名同学积极参加了这次赈灾捐款活动,因不慎,表中数据有一处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
捐款(元) | 10 | 15 | 30 | 50 | 60 | |
人数 | 3 | 6 | 11 | 11 | 13 | 6 |
(1)根据以上信息可知,被污染处的数据为 .
(2)该班捐款金额的众数为 ,中位数为 .
(3)如果用九年级(1)班捐款情况作为一个样本,请估计全校2000人中捐款在40元以上(包括40元)的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
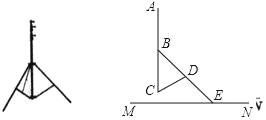
【题目】某数码产品专卖店的一块摄像机支架如图所示,将该支架打开立于地面MN上,主杆AC与地面垂直,调节支架使得脚架BE与主杆AC的夹角∠CBE=45°,这时支架CD与主杆AC的夹角∠BCD恰好等于60°,若主杆最高点A到调节旋钮B的距离为40cm.支架CD的长度为30cm,旋转钮D是脚架BE的中点,求脚架BE的长度和支架最高点A到地面的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
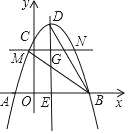
如图,抛物线y=﹣![]() x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
x2+2x+6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,其对称轴与抛物线交于点D.与x轴交于点E.
(1)求点A,B,D的坐标;
(2)点G为抛物线对称轴上的一个动点,从点D出发,沿直线DE以每秒2个单位长度的速度运动,过点C作x轴的平行线交抛物线于M,N两点(点M在点N的左边).
设点G的运动时间为ts.
①当t为何值时,以点M,N,B,E为顶点的四边形是平行四边形;
②连接BM,在点G运动的过程中,是否存在点M.使得∠MBD=∠EDB,若存在,求出点M的坐标;若不存在,请说明理由;
(3)点Q为坐标平面内一点,以线段MN为对角线作萎形MENQ,当菱形MENQ为正方形时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
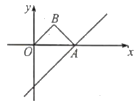
【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠C=120°,AD=2AB=4,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )

A. 1 B. ![]() ﹣1 C.
﹣1 C. ![]() D. 2﹣
D. 2﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2+6mx+n(m>0)与x轴交于A,B两点(点A在点B左侧),顶点为C,抛物线与y轴交于点D,直线BC交y轴于E,S△ABC:S△AEC = 2∶3.
(1)求点A的坐标;
(2)将△ACO绕点C顺时针旋转一定角度后,点A与B重合,此时点O恰好也在y轴上,求抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com