
分析 根据题意画出图形进而利用勾股定理得出AC的长,即可得出此三角形菜地的面积.
解答 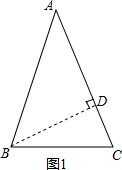 解:如图1所示:过点B作BD⊥AC于点D,
解:如图1所示:过点B作BD⊥AC于点D,
当AB=25m,BC=17m,BD=15m,
则AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=20(m),
故DC=$\sqrt{B{C}^{2}-B{D}^{2}}$=8(m),
则AC=28m,故此三角形菜地的面积为:$\frac{1}{2}$×BD×AC=$\frac{1}{2}$×15×28=210(m2),
如图2所示:过点B作BD⊥AC于点D,
当AB=25m,BC=17m,BD=15m,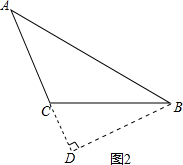
则AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=20(m),
故DC=$\sqrt{B{C}^{2}-B{D}^{2}}$=8(m),
则AC=12m,故此三角形菜地的面积为:$\frac{1}{2}$×BD×AC=$\frac{1}{2}$×15×12=90(m2),
答:此三角形菜地的面积为210m2或90m2.
点评 此题主要考查了勾股定理的应用,根据题意利用分类讨论得出是解题关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
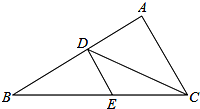 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
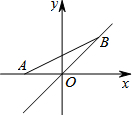 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
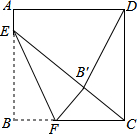 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com