Question

【题目】水果市场中的甲、乙两家商店中都批发同一种水果，批发水果x千克时，在甲、乙两家商店的批发价分别为y1元和y2元，已知y1和y2关于x的函数图象分别为如图所示的折线OAB和射线OC．
（1）请求出y2与自变量x的函数解析式，并写出自变量x的取值范围；
（2）当乙商店的批发价比甲商店的批发价便宜时，根据函数图象直接写出自变量x的取值范围；
（3）如果批发30千克水果时，在甲店批发比在乙店批发便宜50元，求射线AB的函数解析式并写出自变量x的取值范围．

Answer 1

【答案】
（1）解：∵射线OC经过原点，

∴设y2与自变量x的函数关系为y2=k'x（k'≠0），

∵射线OC经过点（20，200），

∴200=20k'，

解得k'=10．

∴y2=10x，自变量x的取值范围是x＞0

（2）解：由图象可知，当0＜x＜20时，在乙店批发比较便宜．
（3）解：∵射线OC过点（20，200），射线OC的表达式是y2=10x，

过点（30，0）作y轴的平行线，交OC于点E，交AB于点F．

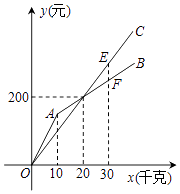
∴E（30，300），F（30，250），

设射线AB的表达式为y1=kx+b，

∴ ，解得 ．

∴射线AB的表达式为y1=5x+100，自变量x的取值范围是x＞10．

【解析】（1）根据射线OC经过点（20，200），即可得到y2与自变量x的函数解析式以及自变量x的取值范围；（2）由图象可知，当0＜x＜20时，在乙店批发比较便宜；（3）过点（30，0）作y轴的平行线，交OC于点E，交AB于点F，即可得到E（30，300），F（30，250），再根据待定系数法进行计算，即可得到射线AB的函数解析式以及自变量x的取值范围．