
 如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且∠OBC=45°,求四边形ABDC的面积.
如图,△ABC内接于⊙O,弦AD⊥BC于E,CF⊥AB于F,交AD于G,BE=3,CE=2,且∠OBC=45°,求四边形ABDC的面积. 分析 过点O作OM⊥BC于M,由垂径定理得出BM=CM=2.5,由∠OBC=45°,得出OM=BM=2.5,由勾股定理求出OB,作ON⊥AD于N,连接OA,由垂径定理得出AN=DN=$\frac{1}{2}$AD,ON=EM=0.5,由勾股定理求出AN名即可得出AD,再由AD⊥BC得出四边ABDC的面积=$\frac{1}{2}$BC•AD,即可得出结果.
解答 解:过点O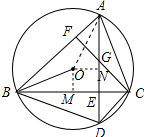 作OM⊥BC于M,如图所示:
作OM⊥BC于M,如图所示:
则BM=CM=$\frac{1}{2}$BC,
∵BE=3,CE=2,
∴BC=5,
∴BM=CM=2.5,
∵∠OBC=45°,
∴OM=BM=2.5,
∴OB=$\sqrt{O{M}^{2}+B{M}^{2}}$=$\frac{5\sqrt{2}}{2}$,
∵BE=3,BM=2.5,
∴EM=3-2.5=0.5,
作ON⊥AD于N,连接OA,
则AN=DN=$\frac{1}{2}$AD,ON=EM=0.5,
∵OA=OB=$\frac{5\sqrt{2}}{2}$,
∴AN=$\sqrt{O{A}^{2}-O{N}^{2}}$=$\frac{7}{2}$,
∴AD=2AN=7,
∵AD⊥BC,
∴四边ABDC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×5×7=$\frac{35}{2}$.
点评 本题考查了垂径定理、勾股定理的综合运用.由垂径定理和勾股定理求出半径是解决问题的突破口,注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | (-1,$\frac{4}{3}$) | B. | (-1,$\frac{3}{4}$) | C. | (-1,$\frac{2}{3}$) | D. | (-1,$\frac{3}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
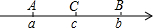 如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置.
如图,已知数轴上点A,B,C所对应的数a,b,c都不为0,且C是AB的中点,如果|a+b|-|a-2c|+|b-2c|-|a+b-2c|=0,试确定原点O的大致位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com