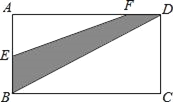
[题目]如图所示.长方形ABCD是“阳光小区内一块空地.已知AB＝(2a+6b)米.BC＝(8a+4b)米．(1)该长方形ABCD的面积是多少平方米?(2)若E为AB边的中点.DF＝BC.现打算在阴影部分种植一片草坪.这片草坪的面积是多少平方米? 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图所示，长方形ABCD是“阳光小区”内一块空地，已知AB＝（2a+6b）米，BC＝（8a+4b）米．

（1）该长方形ABCD的面积是多少平方米？

（2）若E为AB边的中点，DF＝BC，现打算在阴影部分种植一片草坪，这片草坪的面积是多少平方米？

【答案】（1）16a2+56ab+24b2；（2）5a2+ab+b2

【解析】

（1）利用长方形面积计算公式即可求出答案；

（2）先求出AE、AF的长，再利用长方形面积的一半减去三角形AEF的面积即可得到阴影部分的面积.

解：（1）长方形ABCD的面积＝AB×BC

＝（2a+6b）（8a+4b）

＝16a2+56ab+24b2；

（2）由题意得，AF＝AD﹣DF＝BC﹣BC＝（8a+4b）﹣（8a+4b）＝（6a+3b），

AE＝（2a+6b）＝a+3b，

则草坪的面积＝×（16a2+56ab+24b2）﹣×AE×AF

＝×（16a2+56ab+24b2）﹣×（a+3b）（6a+3b）

＝5a2+ab+b2．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A，B两点，其中A，B两点的横坐标分别为﹣1和﹣4，且抛物线过原点．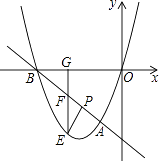

（1）求抛物线的解析式；
（2）在坐标轴上是否存在点C，使△ABC为等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；
（3）若点P是线段AB上不与A，B重合的动点，过点P作PE∥OA，与抛物线第三象限的部分交于一点E，过点E作EG⊥x轴于点G，交AB于点F，若S△BGF=3S△EFP ，求的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，分别以点A和点B为圆心，以大于 AB的长为半径画弧，两弧相交于点M、N，作直线MN，交BC于点D，若△ADC的周长为10，AB=6，则△ABC的周长为（）
A.6
B.12
C.16
D.20

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】矩形纸片ABCD中，AB=5，AC=3，将纸片折叠，使点B落在边CD上的B′处，折痕为AE．在折痕AE上存在一点P到边CD的距离与到点B的距离相等，则此相等距离为．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】数学课上，老师给出了如下问题：

已知：如图1，在Rt△ABC中，∠C=90°，AC=BC，延长CB到点D，∠DBE=45°，点F是边BC上一点，连结AF，作FE⊥AF，交BE于点E．

（1）求证：∠CAF=∠DFE；

（2）求证：AF=EF．

经过独立思考后，老师让同学们小组交流．小辉同学说出了对于第二问的想法：“我想通过构造含有边AF和EF的全等三角形，因此我过点E作EG⊥CD于G（如图2所示），如果能证明Rt△ACF和Rt△FGE全等，问题就解决了．但是这两个三角形证不出来相等的边，好像这样作辅助线行不通．”小亮同学说：“既然这样作辅助线证不出来，再考虑有没有其他添加辅助线的方法．”请你顺着小亮同学的思路在图3中继续尝试，并完成（1）、（2）问的证明．

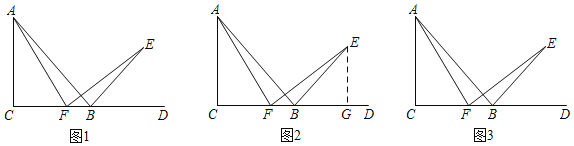
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF=BD，连接BF．

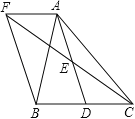
（1）BD与CD有什么数量关系，并说明理由；

（2）当△ABC满足什么条件时，四边形AFBD是矩形？并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】A市和B市分别有库存的某联合收割机12台和6台，现决定开往C市10台和D市8台，已知从A市开往C市、D市的油料费分别为每台400元和800元，从B市开往C市和D市的油料费分别为每台300元和500元．
（1）设B市运往C市的联合收割机为x台，求运费w关于x的函数关系式．
（2）若总运费不超过9000元，问有几种调运方案？
（3）求出总运费最低的调运方案，并求出最低运费．

查看答案和解析>>

科目：初中数学 来源： 题型：