
����Ŀ����ѧ���ϣ���ʦ�������������⣺
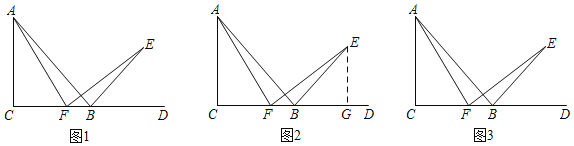
��֪����ͼ1����Rt��ABC�У���C=90�㣬AC=BC���ӳ�CB����D����DBE=45�㣬��F�DZ�BC��һ�㣬����AF����FE��AF����BE�ڵ�E��
��1����֤����CAF=��DFE��
��2����֤��AF=EF��
��������˼������ʦ��ͬѧ��С�齻����С��ͬѧ˵���˶��ڵڶ��ʵ��뷨��������ͨ�����캬�б�AF��EF��ȫ�������Σ�����ҹ���E��EG��CD��G����ͼ2��ʾ���������֤��Rt��ACF��Rt��FGEȫ�ȣ�����ͽ���ˣ�����������������֤��������ȵıߣ������������������в�ͨ����С��ͬѧ˵������Ȼ������������֤���������ٿ�����û���������Ӹ����ߵķ�����������˳��С��ͬѧ��˼·��ͼ3�м������ԣ�����ɣ�1������2���ʵ�֤����
���𰸡���1������������2��������
��������
��1�����ݡ�ͬ�ǵ������ȡ������ɵõ���CAF=��DFE��
��2����AC �Ͻ�ȡAG=BF������FG������ASA�����ж���AGF�ա�FBE�������ó�AF=EF��
֤������1���ߡ�C=90�㣬
���CAF+��AFC=90�㣮
��FE��AF��
���DFE+��AFC=90�㣮
���CAF=��DFE��
��2����ͼ3����AC�Ͻ�ȡAG=BF������FG��
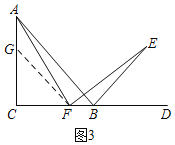
��AC=BC��
��AC-AG=BC-BF����CG=CF��
�ߡ�C=90�㣬
���CGF=��CFG=45�㣮
���AGF=180��-��CGF=135�㣮
�ߡ�DBE=45�㣬
���FBE=180��-��DBE=135�㣮
���AGF=��FBE��
�ɣ�1���ɵã���CAF=��DFE��
���AGF�ա�FBE��ASA����
��AF=EF��


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��b���dz�������k��0����ͼ���㣨1��0���ͣ�0��2����
��1������2��x��3ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m��n=4�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A=��F����C=��D����˵��BD��CE.
�⣺��Ϊ����A=��F��
���ԣ�_____//______��
�����ǣ�____________��
���ԣ���____+��_____=180����
�����ǣ�_______________��
������C=��D��
���ԡ�D+��DEC=180����
�����ǣ�_________________��
���ԣ�______________________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
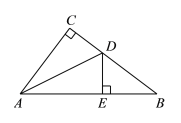
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() �����
�����![]() ��
��![]() ����ô
����ô![]() �ij�Ϊ________
�ij�Ϊ________![]() ��
��![]() �ij�Ϊ_______
�ij�Ϊ_______![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ���ż�ʱ��С��һ������һ���С�γ�ȥ̽��үү�����̺���ү�����ѣ����ϴӼ��������������5ǧ������������Ȼ����������2.5ǧ��үү�ң������үү�ҳ�����������10ǧ����ү�������Ϸ��ؼ��
��1������С����Ϊԭ�㣬��Ϊ��������1����λ���ȱ�ʾ1ǧ�ף��뽫���С�үү�Һ���ү�ҵ�λ�������������Ϸֱ��õ�A��B��C��ʾ������
![]()
��2�����к���ү��������ǧ�ף�
��3����С�γ�ÿǧ����0.08������С��һ�Ҵӳ��������ؼң�С�γ��ĺ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD��������С������һ��յأ���֪AB����2a+6b���ף�BC����8a+4b���ף�
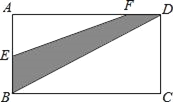
��1���ó�����ABCD������Ƕ���ƽ���ף�
��2����EΪAB�ߵ��е㣬DF��![]() BC���ִ�������Ӱ������ֲһƬ��ƺ����Ƭ��ƺ������Ƕ���ƽ���ף�
BC���ִ�������Ӱ������ֲһƬ��ƺ����Ƭ��ƺ������Ƕ���ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߶�a��b��c��ɵ������β���ֱ�������ε��ǣ� ��
A.a=7��b=24��c=25
B.a= ![]() ��b=4��c=5
��b=4��c=5
C.a= ![]() ��b=1��c=
��b=1��c= ![]()
D.a= ![]() ��b=
��b= ![]() ��c=
��c= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ�������,�ش���������:��һ����ѧʵ��̽�����,Сǿ��A,C���㻭ֱ��AC��ƽ���ı���ABCD�ָ����������(��ͼ1),С�չ�AB,CD���е㻭ֱ��EF,��ƽ���ı���ABCDҲ�ָ����������(��ͼ2).

(1)�����ַָ�������֮��Ĺ�ϵΪ:S1����S2,S3����S4;
(2)��������λͬѧ�ķָ��,����Ϊ��ƽ���ı��ηָ���������������ϵ��ֱ����������,����ͼ3��ƽ���ı����л���һ��;
(3)������ʵ���������,�㷢����ʲô����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
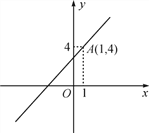
����Ŀ����ͼ����֪��һ�κ���y��kx��3��ͼ����A��1��4����
��1�������һ�κ����Ľ���ʽ��
��2�����жϵ�B����1��5����C��0��3����D��2��1���Ƿ������һ�κ�����ͼ���ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com