
【题目】阅读下面的操作过程,回答后面的问题:在一次数学实践探究活动中,小强过A,C两点画直线AC把平行四边形ABCD分割成两个部分(如图1),小刚过AB,CD的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图2).

(1)这两种分割方法中面积之间的关系为:S1 S2,S3 S4;
(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上面积关系的直线有 条,请在图3的平行四边形中画出一种;
(3)由上述实验操作过程,你发现了什么规律?
科目:初中数学 来源: 题型:
【题目】根据要求回答问题:
(1)已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为; 
(2)[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程; 
(3)[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师给出了如下问题:
已知:如图1,在Rt△ABC中,∠C=90°,AC=BC,延长CB到点D,∠DBE=45°,点F是边BC上一点,连结AF,作FE⊥AF,交BE于点E.
(1)求证:∠CAF=∠DFE;
(2)求证:AF=EF.
经过独立思考后,老师让同学们小组交流.小辉同学说出了对于第二问的想法:“我想通过构造含有边AF和EF的全等三角形,因此我过点E作EG⊥CD于G(如图2所示),如果能证明Rt△ACF和Rt△FGE全等,问题就解决了.但是这两个三角形证不出来相等的边,好像这样作辅助线行不通.”小亮同学说:“既然这样作辅助线证不出来,再考虑有没有其他添加辅助线的方法.”请你顺着小亮同学的思路在图3中继续尝试,并完成(1)、(2)问的证明.
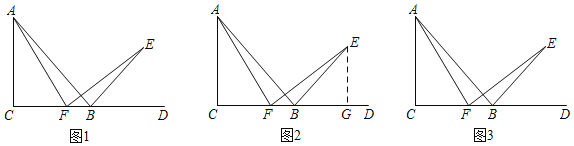
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.
(1)设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形底角的度数为( )
A.50°B.65°C.65°或25°D.50°或40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教研机构为了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查.依据相关数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:


(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2 300名,请估计该校“不重视阅读数学教科书”的初中生人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程交由甲、乙两个工程队来完成,已知甲工程队单独完成需要60天,乙工程队单独完成需要40天
(1)若甲工程队先做30天后,剩余由乙工程队来完成,还需要用时 天
(2)若甲工程队先做20天,乙工程队再参加,两个工程队一起来完成剩余的工程,求共需多少天完成该工程任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-![]() x+12(0<x<24)
x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=![]() x-12(0<x<24)
x-12(0<x<24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com