
【题目】根据要求回答问题:
(1)已知:等边△ABC的边长为4,点P在线段AB上,点D在线段AC上,且△PDE为等边三角形,当点P与点B重合时(如图1),AD+AE的值为; 
(2)[类比探究]在上面的问题中,如果把点P沿BA方向移动,使PB=1,其余条件不变(如图2),AD+AE的值是多少?请写出你的计算过程; 
(3)[拓展迁移]如图3,△ABC中,AB=BC,∠ABC=a,点P在线段BA延长线上,点D在线段CA延长线上,在△PDE中,PD=PE,∠DPE=a,设AP=m,则线段AD、AE有怎样的等量关系?请用含m,a的式子直接写出你的结论. 
【答案】
(1)4
(2)解:AD+AE=3
理由:如图2中,作PK∥BC交AC于K.连接AE.
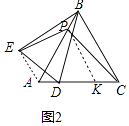
易证△PAK是等边三角形,
由上面题目可知.AE+AD=AK=3
(3)解:如图3中,作PJ⊥AD于J,在AD上取一点K,使得PK=PA.
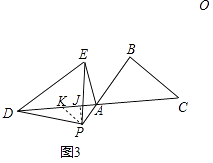
易证∠APK=∠DPE=α,
∵PD=PE,PK=PA,
∴∠DPK=∠EPA,
∴△PDK≌△PEA,
∴DK=AE,
∴AD﹣AE=AK=2AJ=2msin ![]() .
.
∴AD﹣AE=2msin ![]()
【解析】(1)解:如图1中,
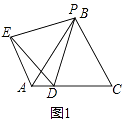
∵△PDE.△PAC都是等边三角形,
∴PE=PD,PA=PC,∠EPD=∠APC=60°,
∴∠EPA=∠DPC,
∴△EPA≌△DPC,
∴AE=CD,
∴AD+AE=AD+DC=AC=4.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某学校七年级三班有50名学生,现对学生最喜欢的球类运动进行了调查,根据调查的结果制作了扇形统计图,如图所示.根据扇形统计图中提供的信息,给出以下结论:
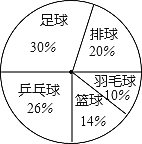
①最喜欢足球的人数最多,达到了15人;
②最喜欢羽毛球的人数最少,只有5人;
③最喜欢排球的人数比最喜欢乒乓球的人数少3人;
④最喜欢乒乓球的人数比最喜欢篮球的人数多6人。
其中正确的结论有
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架长2.5m的梯子斜靠在竖直的墙上,这时梯足到墙的底端距离为0.7m,若梯子顶端下滑0.4m,则梯足将向外移
A、0.6mB、0.7m C、0.8mD、0.9m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)如果点P到点M点N的距离相等,则x= .
(2)数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.
(3)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
解:因为:∠A=∠F,
所以:_____//______,
理由是:____________,
所以:∠____+∠_____=180°,
理由是:_______________,
因为:∠C=∠D,
所以∠D+∠DEC=180°,
理由是:_________________,
所以:______________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的操作过程,回答后面的问题:在一次数学实践探究活动中,小强过A,C两点画直线AC把平行四边形ABCD分割成两个部分(如图1),小刚过AB,CD的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图2).

(1)这两种分割方法中面积之间的关系为:S1 S2,S3 S4;
(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上面积关系的直线有 条,请在图3的平行四边形中画出一种;
(3)由上述实验操作过程,你发现了什么规律?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com