
【题目】李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米.要围成的菜园是如图所示的矩形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )

A. y=-2x+24(0<x<12) B. y=-![]() x+12(0<x<24)
x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=![]() x-12(0<x<24)
x-12(0<x<24)
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的操作过程,回答后面的问题:在一次数学实践探究活动中,小强过A,C两点画直线AC把平行四边形ABCD分割成两个部分(如图1),小刚过AB,CD的中点画直线EF,把平行四边形ABCD也分割成两个部分(如图2).

(1)这两种分割方法中面积之间的关系为:S1 S2,S3 S4;
(2)根据这两位同学的分割方法,你认为把平行四边形分割成满足以上面积关系的直线有 条,请在图3的平行四边形中画出一种;
(3)由上述实验操作过程,你发现了什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 . 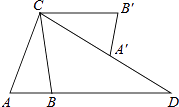
查看答案和解析>>
科目:初中数学 来源: 题型:
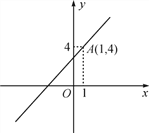
【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”前夕,某玩具经销商用去2350元购进A,B,C三种新型的电动玩具共50套,并且购进的三种玩具都不少于10套,设购进A种玩具x套,B种玩具y套,三种电动玩具的进价和售价如表所示
型 号 | A | B | C |
进价(元/套) | 40 | 55 | 50 |
售价(元/套) | 50 | 80 | 65 |
(1)用含x、y的代数式表示购进C种玩具的套数;
(2)求y与x之间的函数关系式;
(3)假设所购进的这三种玩具能全部卖出,且在购销这种玩具的过程中需要另外支出各种费用200元.
①求出利润P(元)与x(套)之间的函数关系式;②求出利润的最大值,并写出此时三种玩具各多少套.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC的直角边为1,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边.画第三个Rt△ADE,…,依此类推直到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为 . 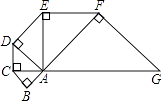
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com