
����Ŀ����һ�����ǰ��е�����ֱ�����dzߵ�ֱ�Ƕ���O����ͼ��ʽ������һ��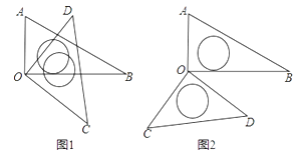
��1����ͼ��1������BOD=35�㣬���AOC�Ķ���������AOC=135�㣬���BOD�Ķ�����
��2����ͼ��2������AOC=140�㣬���BOD�Ķ���
��3�������AOC���BOD�Ĵ�С��ϵ�������ͼ��1��˵�����ɣ�
��4�����dz�AOB�����������dz�COD��OD����OA���غϣ�Ȼ���Ƶ�O��˳ʱ�����ʱ�뷽������ת��һ���Ƕȣ�����AOD��0�㣼��AOD��90�㣩���ڶ��ٶ�ʱ�����������dz߸���һ�����ഹֱ��ֱ��д����AOD�Ƕ����п��ܵ�ֵ������˵������
���𰸡�
��1���⣺����BOD=35�㣬�ߡ�AOB=��COD=90�㣬
���AOC=��AOB+��COD����BOD=90��+90�㩁35��=145�㣬
����AOC=135�㣬
���BOD=��AOB+��COD����AOC=90��+90�㩁135��=45��
��2���⣺��ͼ2������AOC=140�㣬
���BOD=360�㩁��AOC����AOB����COD=40��
��3���⣺��AOC���BOD������
�ߡ�AOD+��BOD+��BOD+��BOC=180�㣮
�ߡ�AOD+��BOD+��BOC=��AOC��
���AOC+��BOD=180�㣬
����ACB���DCE������
��4���⣺OD��ABʱ,��AOD=30��CD��OBʱ,��AOD=45��,
CD��ABʱ,��AOD=75��
OC��ABʱ,��AOD=60
����AOD�Ƕ����п��ܵ�ֵΪ30�㡢45�㡢60�㡢75��
����������1��ץס��֪��ABO�͡�DCO����ֱ�������Σ�����һ�����ݡ�AOC=��AOB+��COD����BOD�����㼴�������AOC�Ķ����������������ݡ�BOC=��DOC-��BOD���ٸ��ݡ�AOC=��BOC+��AOB�����㼴�ɵó���AOC�Ķ���������AOC=135�㣬����һ�����ݡ�BOD=��AOB+��COD����AOC�����㼴�ɵó��𰸣������������ݡ�AOD=��AOC-��DOC���ٸ��ݡ�BOD=��AOB-AOD�����㼴�ɵó��𰸡�
��2���۲�ͼ��2���ɵó���BOD=360�㩁��AOC����AOB����COD������AOC���BOD���������㼴�ɡ�
��3��������֪���ͼ����֤��ACB���DCE������
��4���ֱ����OD��ABʱ��CD��OBʱ��CD��ABʱ��OC��ABʱ�ֱ������AOD�Ķ������ɡ�


 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD���ı���A��B��C��D�������ǵ��ܳ��ֱ�Ϊ5m��3m����S�ı���ABCD��S�ı���A��B��C��D��=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
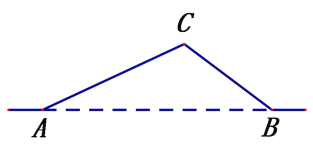
����Ŀ����ͼ����A�ص�B�صĹ�·�辭��C�أ�ͼ��AC=10ǧ�ף���CAB=25�㣬��CBA=37��. ����й滮����Ҫ������A��B����֮����һ����ֱ�Ĺ�·.
��1�����ֱ��Ĺ�·AB�ij���
��2���ʹ�·��ֱ��ö�·�̱�ԭ�������˶���ǧ�ף���sin25���0.42��cos25���0.91,sin37���0.60��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ��������������ͼ����ͬ��������A��3��m����B��n��2������ôһ���У�������
A.m��0��n��0B.m��0��n��0C.m��0��n��0D.m��0��n��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽�AB��N����AC��M�� 
��1������B=70�㣬���NMA�Ķ����� ��
��2������MB����AB=8cm����MBC���ܳ���14cm��
����BC�ij���
����ֱ��MN���Ƿ���ڵ�P��ʹ��P��B��C���ɵġ�PBC���ܳ�ֵ��С�������ڣ������P��λ�ò����PBC���ܳ���Сֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A��1��2����B��3��1����C����2����1���� 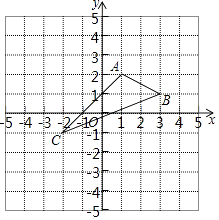
��1����ͼ��������ABC����x��ĶԳ�ͼ�Ρ�A1B1C1 ��
��2��д����A1 �� B1 �� C1�����ֱ꣨��д�𰸣�
A1
B1
C1
��3�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��AB��CD��ֱ��l��ֱ��AB��CD�ཻ�ڵ�E��F����P������EA�ϵ�һ�����㣨�������˵�E��������EPF��PF�۵���ʹ����E���ڵ�Q��.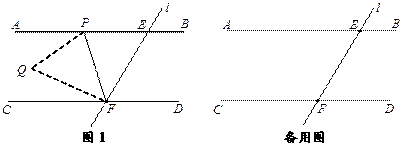
��1������PEF=48�㣬��Qǡ���������е�һ��ƽ�����ϣ���ֱ��д����EFP�Ķ���.
��2������PEF��75�㣬��CFQ�� ![]() ��PFC�����EFP�Ķ���.
��PFC�����EFP�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���һ��˫�米��������������60%��ۣ�Ȼ���ٰ�8�ۣ���۵�80%�����ۣ������̳�ÿ����һ������Ϳ�Ӯ��14Ԫ����������Ľ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com