
【题目】如图1,直线AB∥CD,直线l与直线AB、CD相交于点E、F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.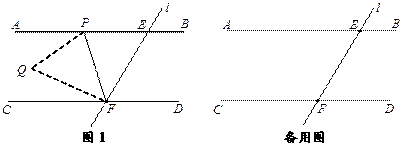
(1)若∠PEF=48°,点Q恰好落在其中的一条平行线上,请直接写出∠EFP的度数.
(2)若∠PEF=75°,∠CFQ= ![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
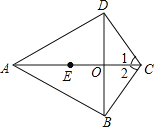
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.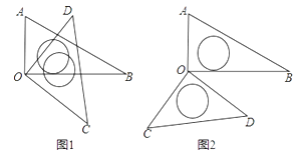
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数。
(2)如图(2)若∠AOC=140°,求∠BOD的度数
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 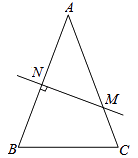
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯从报社以每份0.4元的价格购进了a份报纸,以每份0.5元的价格售出了b份报纸,剩余的以每份0.2元的价格退回报社,则张大伯卖报收入元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com