练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB、CD交于点O，∠1=∠2，∠3：∠1=8：1，求∠4的度数．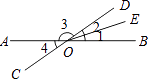

    【答案】解：∵平分∠BOD， ∴∠1=∠2，
    ∵∠3：∠1=8：1，
    ∴∠3=8∠1．
    ∵∠1+∠2+∠3=180°，
    ∴∠1+∠1+8∠1=180°，
    解得∠1=18°，
    ∴∠4=∠1+∠2=36°
    【解析】根据角平分线的定义得∠1=∠2，由∠3：∠1=8：1得∠3=8∠1．根据平角的定义有∠1+∠2+∠3=180°，则∠1+∠1+8∠1=180°，可解得出∠1=18°，而根据对顶角相等有∠4=∠1+∠2，然后把∠1、∠2的度数代入计算即可．
    【考点精析】解答此题的关键在于理解对顶角和邻补角的相关知识，掌握两直线相交形成的四个角中，每一个角的邻补角有两个，而对顶角只有一个．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】魔术师为大家表演魔术．他请观众想一个数，然后将这个数按以下步骤操作：

    魔术师立刻说出观众想的那个数．
    （1）如果小明想的数是﹣1，那么他告诉魔术师的结果应该是；
    （2）如果小聪想了一个数并告诉魔术师结果为93，那么魔术师立刻说出小聪想的那个数是；
    （3）观众又进行了几次尝试，魔术师都能立刻说出他们想的那个数，请你说出其中的奥妙．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个角的余角的3倍比它的补角的2倍少120°，则这个角的度数为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°. 因城市规划的需要，将在A、B两地之间修建一条笔直的公路.

    （1）求改直后的公路AB的长；

    （2）问公路改直后该段路程比原来缩短了多少千米？（sin25°≈0.42，cos25°≈0.91,sin37°≈0.60，tan37°≈0.75）

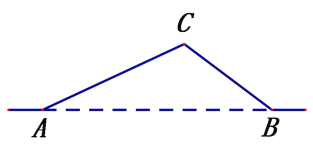
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程：已知：直线l和l外一点P．（如图1）求作：直线l的垂线，使它经过点P．作法：如图2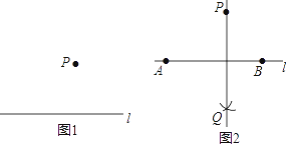

    ①在直线l上任取两点A，B；
    ②分别以点A，B为圆心，AP，BP长为半径作弧，两弧相交于点Q；
    ③作直线PQ． 所以直线PQ就是所求的垂线．
    请回答：该作图的依据是

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个正比例函数的图象经过不同象限的两点A（3，m），B（n，2），那么一定有（　　）

    A.m＞0，n＞0B.m＜0，n＜0C.m＞0，n＜0D.m＜0，n＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交AC于M．

    （1）若∠B=70°，则∠NMA的度数是 ．
    （2）连接MB，若AB=8cm，△MBC的周长是14cm．
    ①求BC的长；
    ②在直线MN上是否存在点P，使由P，B，C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，直线AB∥CD，直线l与直线AB、CD相交于点E、F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处.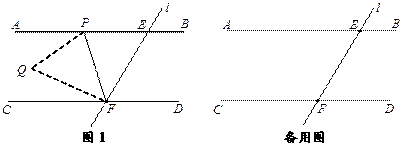

    （1）若∠PEF=48°，点Q恰好落在其中的一条平行线上，请直接写出∠EFP的度数.
    （2）若∠PEF＝75°，∠CFQ＝ ∠PFC，求∠EFP的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在△ABC中，∠A=90°，BD是∠ABC的平分线，DE是BC的垂直平分线，则∠C= ．

    查看答案和解析>>

    同步练习册答案