
分析 设等腰三角形的两个内角的度数分别是ax、bx.由该三角形是钝角三角形得到该等腰三角形的三个内角的度数分别是ax、ax、bx.依据钝角三角形的定义来求b:a的取值范围.
解答 解:设等腰三角形的两个内角的度数分别是ax、bx.
∵a<b,且该等腰三角形是钝角三角形,
∴该等腰三角形的三个内角的度数分别是ax、ax、bx.
∴2ax<90°,即ax<45°,
bx>90°,
∴ax:bx<$\frac{1}{2}$,即b:a的取值范围是:$\frac{b}{a}$>2.
故答案是:$\frac{b}{a}$>2.
点评 本题考查了等腰三角形的性质.此题有限制性条件a<b、这个三角形是钝角三角形可以判定b是顶角.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:解答题
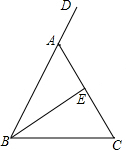 如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上一点,E是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
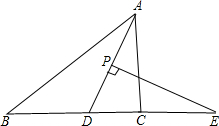 在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).
在△ABC中,AD平分∠BAC,P为线段AD上的一个点,PE⊥AD交直线BC于点E(∠ABC、∠ACB的大小不确定).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
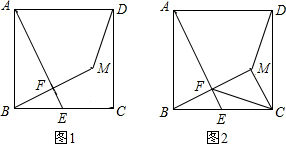
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
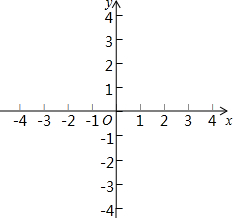 平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.
平面直角坐标系中,标出并顺次连结A(-2,1),B(-2,-1),C(2,1),D(2,3)各点,你会得到一个什么图形?试求出该图形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
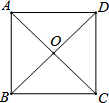 如图,正方形ABCD的对角线交于点O,点F是BC的中点.
如图,正方形ABCD的对角线交于点O,点F是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com