
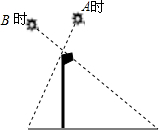
 如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.
如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米. 分析 如图,∠CPD=90°,QC=4m,QD=9m,利用等角的余角相等得到∠QPC=∠D,则可判断Rt△PCQ∽Rt△DPQ,然后利用相似比可计算出PQ.
解答 解: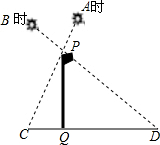 如图,∠CPD=90°,QC=4m,QD=9m,
如图,∠CPD=90°,QC=4m,QD=9m,
∵PQ⊥CD,
∴∠PQC=90°,
∴∠C+∠QPC=90°,
而∠C+∠D=90°,
∴∠QPC=∠D,
∴Rt△PCQ∽Rt△DPQ,
∴$\frac{PQ}{QD}$=$\frac{QC}{PQ}$,即$\frac{PQ}{9}$=$\frac{4}{PQ}$,
∴PQ=6,
即旗杆的高度为6m.
故答案为6.
点评 本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.也考查了相似三角形的判定与性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
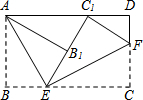 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
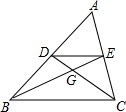 如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,
如图,点D,E分别是△ABC的边AB,AC的中点,BE交CD于G点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
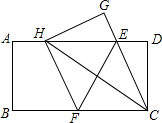 如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com