
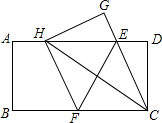
 如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )
如图,在一张矩形纸片ABCD中,AB=2,BC=4,点E、F分别在AD、BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,下列三个结论:①EF垂直平分HC;②EC平分∠DCH;③当点H与点A重合时,BF=$\frac{3}{2}$.其中正确的结论是( )| A. | ①②③ | B. | ①② | C. | ②③ | D. | ①③ |
分析 先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的值,判断出③正确.
解答 解:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,故①正确;
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,故②错误;
点H与点A重合时,设BF=x,则AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即22+x2=(4-x)2,
解得x=$\frac{3}{2}$,故③正确.
故选D.
点评 本题考查了翻折变换的性质,菱形的判定与性质,勾股定理的应用,难点在于灵活运用菱形的判定与性质与勾股定理等其它知识有机结合.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
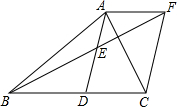 已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.
已知,如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交与BE的延长线于点F,且AF=DC,连结CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
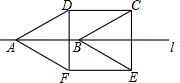 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
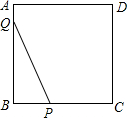 如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.
如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com