
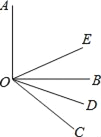
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
【答案】(1)45° ;(2)![]() α;(3)∠DOE的大小与∠BOC的大小无关.
α;(3)∠DOE的大小与∠BOC的大小无关.
【解析】试题分析:(1)首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(2)方法与(1)相同,首先计算出∠AOC的度数,然后再根据角平分线的性质可得∠COE=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
∠BOC,根据∠DOE=∠COE-∠COD代入角度计算即可;
(3)根据(1)(2)的结果可得∠DOE的大小与∠BOC的大小无关.
试题解析:(1)∵∠AOB=90°,∠BOC=38°
∴∠AOC=∠AOB+∠BOC=90°+38°=128°
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() ×128°=64°
×128°=64°
∠COD=![]() ∠BOC=
∠BOC=![]() ×38°=19°
×38°=19°
∴∠DOE=∠COE﹣∠COD=64°﹣19°=45°
(2)∵∠AOB=α,∠BOC=β,
∴∠AOC=∠AOB+∠BOC=α+β,
又∵OE,OD分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠AOC=
∠AOC=![]() (α+β)
(α+β)
∠COD=![]() ∠BOC=
∠BOC=![]() β
β
∴∠DOE=∠COE﹣∠COD=![]() (α+β)﹣
(α+β)﹣![]() β=
β=![]() α+
α+![]() β﹣
β﹣![]() =
=![]() α;
α;


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的 概率是![]() ;中再放进1个黑球,这时取得黑球的概率变为
;中再放进1个黑球,这时取得黑球的概率变为![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y个白球进行摸球游戏。约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
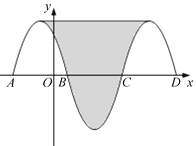
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(![]() , 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .
, 0),点B(0,1),作第一个正方形OA1C1B1且点A1在OA上,点B1在OB上,点C1在AB上;作第二个正方形A1A2C2B2且点A2在A1A上,点B2在A1C2上,点C2在AB上…,如此下去,则点Cn的纵坐标为 .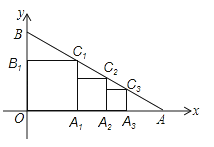
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com