
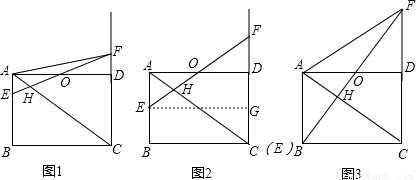
��ͼ������ABCD�У���E��F�ֱ��A��D����ͬʱ����������ͬ���ٶ���ֱ���˶�.��E���߶�AB���˶�����F������CD�˶�������EF��AF��AC��EF�ֱ�AD��AC �ڵ�O��H��
��1����֤��EO=OF��
��2������E�˶���ʲôλ��ʱ��EF=AC,�ڱ���ͼ1�л���ͼ�β�˵�����ɣ�
��3������E�˶���ʲôλ��ʱ����FAD=��CAD,�ڱ���ͼ2�л���ͼ�β�˵�����ɣ���ʱ���ı���CDOH�����ΪS ���ı���ABCF�����ΪS
���ı���ABCF�����ΪS ����ֱ��д��S
����ֱ��д��S ��S
��S ��ֵ��
��ֵ��

��1��֤����������
��2����E��AB���е㣮���ɼ�������
��3����E���B�غϣ�S1��S2=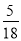 ��
��
��������
�����������1���ɾ��ε����ʾͿ��Եó���EAD=��FDA=90�㣬����AE=DF�Ϳ��Եó���AOE�ա�DOF�Ϳ��Եó����ۣ�
��2����EG��CD��G���ɾ��ε����ʾͿ��Եó���EGF�ա�ADC�Ϳ��Եó����ۣ�
��3����ͼ3������FAD=��CAD�Ϳ��Եó���ADF�ա�ADC�Ϳ��Եó�DF=DC���ó�AF=CD=AB���ó�������
�����������1��֤������ͼ1�����ı���ABCD�Ǿ��Σ�
��AD=BC��AB=DC����DAB=��ADC=��B=��BCD=90�㣮
����AOE����DOF��
 ��
��
���AOE�ա�DOF��AAS����
��EO=OF��
��2����E��AB���е㣮
���ɣ���ͼ2����EG��CD��G��
���EGF=90�㣬
���ı���AEGD�Ǿ��Σ�
��EG=AD��AE=DG��
��FD=DG��
��DG= FG��
FG��
��Rt��ADC��Rt��EGF��
 ��
��
��Rt��ADC��Rt��EGF��HL����
��FG=DC��
��DG= DC��
DC��
��AE= AB��
AB��
����E��AB���е㣻
��3����E���B�غ�
���ɣ�����ADF����ADC��
 ��
��
���ADF�ա�ADC��ASA����
��FD=CD��
��AE=CD��
��AE=AB��
����E���B�غϣ�
���ı���ABCD�Ǿ���
��AD��BC��AB��CD��
���AOH�ס�CBH����AHB�ס�
��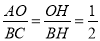 ��
��
��S��AOH��S��CBH=1��4��S��OH��S��ABH=1��2��
��S��AOH=a����S��ABH=2a��S��CBH=4a��
��S��ABC=6a��S��ADC=6a��
��S�ı���ABCF=18a��S�ı���CDOH=5a��
��S�ı���CDOH��S�ı���ABCF=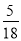 ��
��
��S1��S2=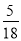 ��
��
 ��
��
���㣺�ı����ۺ�����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭��ʡ�Ͼ����������п�һģ��ѧ�Ծ��������棩 ���ͣ�ѡ����
����(a3b)2��(ab)2�Ľ���� �� ��
A��a3 B��a4 C��a3b D��a4b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭��ʡ�˻��о��꼶�п������ľ���Ӧ��ѵ������һģ����ѧ�Ծ��������棩 ���ͣ������
��֪����x��һԪ���η���x2+bx+b��1=0��������ȵ�ʵ��������b��ֵ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭��ʡ�˻��о��꼶�п������ľ���Ӧ��ѵ������һģ����ѧ�Ծ��������棩 ���ͣ�ѡ����
������С��ͬ������ˮƽ���Ͽ���һ�������ͼ��ʾ�ļ����壬��ü����������ͼ�ǣ�������

A.���������Բ B.�������е�Բ
C.�����ཻ��Բ D.�������е�Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭��ʡ�˻��о��꼶�п������ľ���Ӧ��ѵ������ģ����ѧ�Ծ��������棩 ���ͣ������
��ͼ��ij�㳡һ����AB��һ����CD�̶���CD������37��нǣ���CB��4�ף�
(1)�����CD�ij��ȣ�
(2)��AD��2.1�ף��ƵĶ���E����A��1.8�ף�����EAB��120�㣬��ƵĶ���E�����������ף� (�ο����ݣ�sing37���0.60��cos37���0.80��tan37���0.75)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭��ʡ�˻��о��꼶�п������ľ���Ӧ��ѵ������ģ����ѧ�Ծ��������棩 ���ͣ������
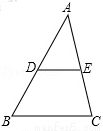
��ͼ������ABC�У���D��E�ֱ���AB��AC���е㣬��A=50�㣬��ADE=60�㣬����C= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭�մ����ׯ�ڶ����о��꼶��ѧ�ڵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
ij���������ɺ�����ƽ����ÿ�������ص�������ˮ60�֣��йز��Ž������𣬴Ӽס�����ˮ����������ˮ����ˮ�㣬�׳�ÿ�����ɵ���40�֣��ҳ�ÿ�����ɵ���45�֣�����ˮ����ˮ����ƽ������ˮ���·�̺��˷����±���
| ����ƽ������ˮ���·�̣�ǧ�ף� | �˷ѣ�Ԫ/�֡�ǧ�ף� |
�׳� | 20 | 4 |
�ҳ� | 14 | 5 |
��1����ij�����ˮ�����˷�Ϊ4450Ԫ����Ӽס�����ˮ���������˶��ٶ�����ˮ?
��2����Ӽ׳���������ˮx�֣����˷�ΪWԪ����д��W����x�ĺ�����ϵʽ����ȷ��x��ȡֵ��Χ���������ŵ��˷�������ʹÿ������˷���ʡ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013-2014ѧ�꽭������������ѧ���꼶3���¿���ѧ�Ծ��������棩 ���ͣ������
�ֽ���ʽ��x3��9x= ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com