
【题目】如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=![]() 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
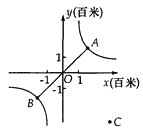
(1)发现C船时,A、B、C三船所在位置的坐标分别为A(_______,_______)、B(_______,_______)和C(_______,_______);
(2)发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.
【答案】(1)A(2,2),B(-2,-2),C(2![]() ,-2
,-2![]() );(2)教练船没有最先赶到,理由见详解.
);(2)教练船没有最先赶到,理由见详解.
【解析】
(1)A、B两点直线y=x上和双曲线y=![]() ,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2
,列方程组可求A、B两点坐标,在依题意判断△ABC为等边三角形,OA=2![]() ,则OC=
,则OC=![]() OA=2
OA=2![]() ,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标;
,过C点作x轴的垂线CE,垂足为E,利用OC在第四象限的角平分线上求OE,CE,确定C点坐标;
(2)分别求出AC、OC的长,分别表示教练船与A、B两船的速度与时间,比较时间的大小即可.
解:(1)CE⊥x轴于E,解方程组![]()
得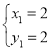 ,
,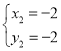
∴A(2,2),B(-2,-2),
在等边△ABC中可求OA=2![]() ,
,
则OC=![]() OA=2
OA=2![]() ,
,
在Rt△OCE中,![]() ,
,
∴C(2![]() ,-2
,-2![]() );
);
(2)作AD⊥x轴于D,连AC、BC和OC,

∵A(2,2),
∴∠AOD=45°,AO=2![]() ,
,
∵C在O的东南45°方向上,
∴∠AOC=45°+45°=90°,
∵AO=BO,∴AC=BC,
又∵∠BAC=60°,
∴△ABC为正三角形,
∴AC=BC=AB=2AO=4![]() ,
,
∴![]() ,
,
由条件设教练船的速度为3m,A、B两船的速度都为4m,
则教练船所用时间为![]() ,A、B两船所用时间均为
,A、B两船所用时间均为![]() =
=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() >
>![]() ;
;
∴教练船没有最先赶到.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
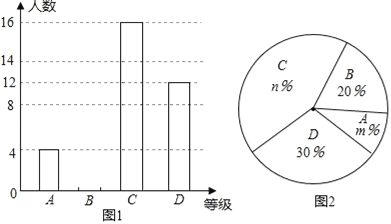
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在平行四边形![]() 中,点
中,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
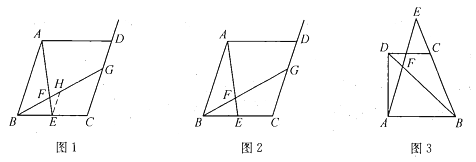
(1)尝试探究
在图1中,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则
,则![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 和
和![]() 的数量关系是______,
的数量关系是______,![]() 的值是______;
的值是______;
(2)类比延伸
如图2,在原题的条件下,当![]() 时,参照问题(1)的研究结论,请你猜想
时,参照问题(1)的研究结论,请你猜想![]() 的值(用含
的值(用含![]() 的代数式表示),并证明你的猜想;
的代数式表示),并证明你的猜想;
(3)拓展迁移
如图3,梯形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 和
和![]() 相交于点
相交于点![]() ,当
,当![]() ,
,![]() 时,请你求出
时,请你求出![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
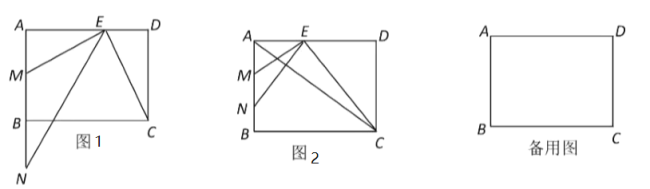
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在射线
在射线![]() 上,且
上,且![]() 是
是![]() 和
和![]() 的比例中项.
的比例中项.
(1)如图1,求证:![]() ;
;
(2)如图2,当点![]() 在线段
在线段![]() 之间,联结
之间,联结![]() ,且
,且![]() 与
与![]() 互相垂直,求
互相垂直,求![]() 的长;
的长;
(3)联结![]() ,如果
,如果![]() 与以点
与以点![]() 、
、![]() 、
、![]() 为顶点所组成的三角形相似,求
为顶点所组成的三角形相似,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过![]() ,
,![]() 及原点
及原点![]() ,顶点为
,顶点为![]() .
.
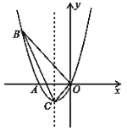
(1)求抛物线的函数解析式;
(2)设点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,且以
在抛物线的对称轴上,且以![]() 、
、![]() 、
、![]() ,
,![]() 为顶点,
为顶点,![]() 为边的四边形是平行四边形,求点
为边的四边形是平行四边形,求点![]() 的坐标;
的坐标;
(3)![]() 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .是否存在这样的点
.是否存在这样的点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC 纸板中, AB =AC=5 , BC = 2 ,P为AB上一点,过P沿直线剪下一个与△ABC 相似的小三角形纸板,恰有 3 种不同的剪法,那么BP长可以为( ).

A.3.6B.2.6C.1.6D.0.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
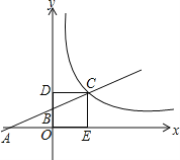
【题目】如图,直线y1=kx+1分别交x轴,y轴于点A.B,交反比例函数y2=![]() (x>0)的图象于点C,CD⊥y轴于点D,CE⊥x轴于点E,S△OAB=1,
(x>0)的图象于点C,CD⊥y轴于点D,CE⊥x轴于点E,S△OAB=1,![]() =
=![]() .
.
(1)点A的坐标为______;
(2)求直线和反比例函数的解析式;
(3)根据图象直接回答:在第一象限内,当x取何值时,y1≥y2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com