Question

【题目】如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ=PQ，PR=PS，则下列四个结论：①PA平分∠BAC；②AS=AR；③QP∥AR；④△BRP≌△CSP，其中结论正确的序号为（ ）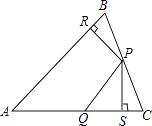

A.①②③
B.①②④
C.②③④
D.①②③④

Answer 1

【答案】D
【解析】解：∵PR⊥AB，PS⊥AC，PR=PS，
∴点P在∠A的平分线上，∠ARP=∠ASP=90°，
∴∠SAP=∠RAP，
在Rt△ARP和Rt△ASP中，由勾股定理得：AR2=AP2﹣PR2 ， AS2=AP2﹣PS2 ，
∵AP=AP，PR=PS，
∴AR=AS，∴②正确；
∵AQ=QP，
∴∠QAP=∠QPA，
∵∠QAP=∠BAP，
∴∠QPA=∠BAP，
∴QP∥AR，∴③正确；
∵△ABC是等边三角形，
∴∠B=∠CAB=60°，AB=AC，
∵∠QAP=∠BAP，
∴BP=CP，
∵QP∥AB，
∴∠QPC=∠B=60°=∠C，
∴PQ=CQ，
∴△PQC是等边三角形，
∴PQ=CP=BP，∠SQP=60°=∠B，
∵PR⊥AB，PS⊥AC，
∴∠BRP=∠PSQ=90°，
在△BRP和△QSP中，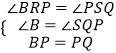
，
∴△BRP≌△QSP，∴④正确；
连接RS，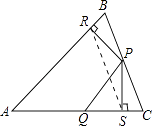

∵PR=PS，
∴点P在RS的垂直平分线上，
∵AS=AR，
∴点A在RS的垂直平分线上，
∴AP垂直平分RS，∴①正确．
所以答案是：D．
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案，需要熟知定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．