
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
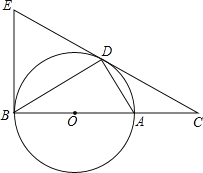
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)见解析;(3)BE的长为5.
【解析】
(1)通过相似三角形(△ADC∽△DBC)的对应边成比例来证得结论.
(2)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可.
(3)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可.
解:(1)证明:∵∠CDA=∠CBD,∠C=∠C,
∴△ADC∽△DBC,
∴![]() ,即CD2=CACB.
,即CD2=CACB.
(2)证明:如图,连接OD,
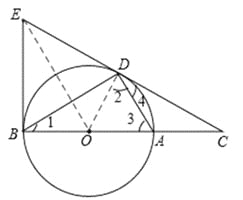
∵AB是⊙O的直径,
∴∠ADB=90°.
∴∠1+∠3=90°.
∵OA=OD,
∴∠2=∠3.
∴∠1+∠2=90°.
又∵∠CDA=∠CBD,即∠4=∠1,
∴∠4+∠2=90°,即∠CDO=90°.
∴OD⊥OA.
又∵OA是⊙O的半径,
∴CD是⊙O的切线.
(3)如图,连接OE,
∵EB、CD均为⊙O的切线,
∴ED=EB,OE⊥DB.
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°.
∴∠ABD=∠OEB.
∴∠CDA=∠OEB.
∵tan∠CDA=![]() ,
,
∴![]() .
.
∵Rt△CDO∽Rt△CBE,
∴![]() .
.
∵BC=12,
∴CD=8.
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,解得x=5.
∴BE的长为5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了解全校学生参加社会实践活动情况,随机调查了部分学生一学期参加社会实践活动的时间(单位:天),并用得到的数据绘制了统计图(1)和图 (2). 请根据图中提供的信息,回答下列问题:

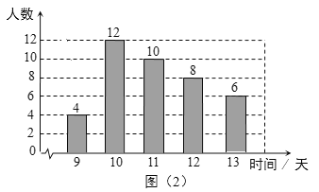
![]()
(1) 本次随机调查的学生人数是_______,图(1)中m的值是_______;
(2)求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数;
(3)该校有480名学生,根据获取的社会实践活动时间样本数据,估计该校一学期社会实践活动时间大于10 天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() .
.![]() ,
,![]() 分别是对角线
分别是对角线![]() ,
,![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() ,
,![]() 之间的距离最短为( )
之间的距离最短为( )
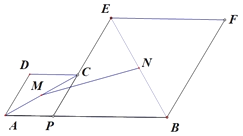
A.![]() B.
B.![]() C.4D.3
C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和小康想用标杆来测量河对岸的树AB的高,两人在确保无安全隐患的情况下,小康在F处竖立了一根标杆EF,小华走到C处时,站立在C处看到标杆顶端E和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离DC=16米;然后,小华在C处蹲下,小康平移标杆到H处时,小华恰好看到标杆顶端G和树的顶端B在一条直线上,此时测得小华的眼睛到地面的距离MC=0.8米.已知EF=GH=2.4米,CF=2米,FH=1.6米,点C、F、H、A在一条直线上,点M在CD上,CD⊥AC,EF⊥AC,CH⊥AC,AB⊥AC,根据以上测量过程及测量数据,请你求出树AB的高度.
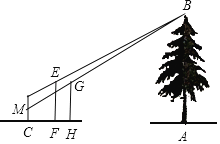
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
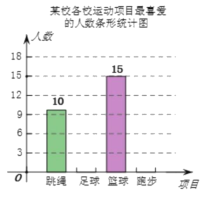
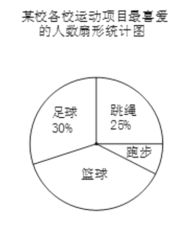
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,“篮球”部分所对应的圆心角度数为__ ;
(4)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受新型冠状病毒疫情的影响,某市教育主管部门在推迟各级学校返校时间的同时安排各个学校开展形式多样的网络教学,学校计划在每周三下午15:30至16:30为学生提供以下四类学习方式供学生选择:在线阅读、微课学习、线上答疑、在线讨论,为了解学生的需求,通过网络对部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
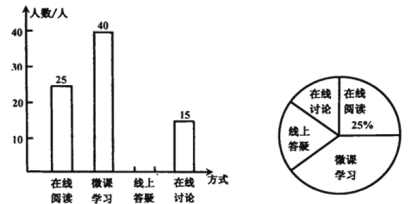
(1)求本次调查的学生总人数;
(2)请求出“线上答疑”在扇形统计图中的圆心角度数;
(3)笑笑和瑞瑞同时参加了网络学习,请求出笑笑和瑞瑞选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
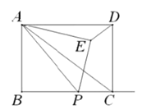
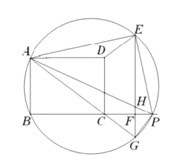
【题目】如图,在矩形![]() 中
中![]() ,
,![]() ,连结
,连结![]() ,点
,点![]() 在射线
在射线![]() 上,以
上,以![]() 为边在
为边在![]() 上方作
上方作![]() ,作
,作![]() ,连结
,连结![]() .
.
(1)当点![]() 在线段
在线段![]() 上时,证明:
上时,证明:![]() ;
;
(2)若![]() 时,求
时,求![]() 的面积;
的面积;
(3)![]() 的外接圆交射线
的外接圆交射线![]() 于点
于点![]() ,作直线
,作直线![]() 交直线
交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com