
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() .
.![]() ,
,![]() 分别是对角线
分别是对角线![]() ,
,![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() ,
,![]() 之间的距离最短为( )
之间的距离最短为( )
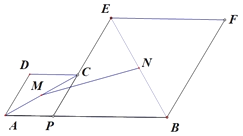
A.![]() B.
B.![]() C.4D.3
C.4D.3
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
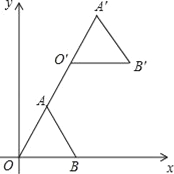
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,四边形OABC是正方形,点A,C 在坐标轴上,点B(![]() ,
,![]() ),P是射线OB上一点,将
),P是射线OB上一点,将![]() 绕点A顺时针旋转90°,得
绕点A顺时针旋转90°,得![]() ,Q是点P旋转后的对应点.
,Q是点P旋转后的对应点.
(1)如图(1)当OP = ![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)如图(2),设点P(![]() ,
,![]() )(
)(![]() ),
),![]() 的面积为S. 求S与
的面积为S. 求S与![]() 的函数关系式,并写出当S取最小值时,点P的坐标;
的函数关系式,并写出当S取最小值时,点P的坐标;
(3)当BP+BQ = ![]() 时,求点Q的坐标(直接写出结果即可)
时,求点Q的坐标(直接写出结果即可)
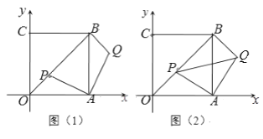
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
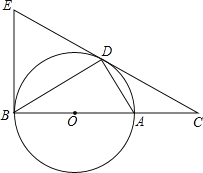
(1)求证:CD2=CACB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
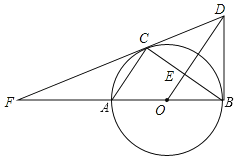
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 交于
交于![]() ,B两点,与y轴交于点
,B两点,与y轴交于点![]() .
.
(1)求抛物线的解析式;
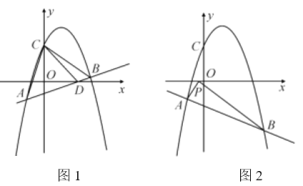
(2)如图1,直线AB交![]() 轴于点D,且
轴于点D,且![]() ,求点B的坐标;
,求点B的坐标;
(3)如图2,当![]() 时,在x轴上有且只有一点P,使
时,在x轴上有且只有一点P,使![]() ,求k的值.
,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com