
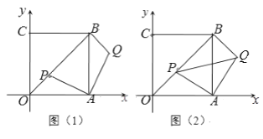
【题目】平面直角坐标系中,四边形OABC是正方形,点A,C 在坐标轴上,点B(![]() ,
,![]() ),P是射线OB上一点,将
),P是射线OB上一点,将![]() 绕点A顺时针旋转90°,得
绕点A顺时针旋转90°,得![]() ,Q是点P旋转后的对应点.
,Q是点P旋转后的对应点.
(1)如图(1)当OP = ![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)如图(2),设点P(![]() ,
,![]() )(
)(![]() ),
),![]() 的面积为S. 求S与
的面积为S. 求S与![]() 的函数关系式,并写出当S取最小值时,点P的坐标;
的函数关系式,并写出当S取最小值时,点P的坐标;
(3)当BP+BQ = ![]() 时,求点Q的坐标(直接写出结果即可)
时,求点Q的坐标(直接写出结果即可)
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据正方形的性质、解直角三角形可得![]() ,
,![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,从而可得
,从而可得![]() ,由此即可得出答案;
,由此即可得出答案;
(2)先根据正方形的性质得出![]() ,
,![]() ,再根据旋转的性质、勾股定理可得
,再根据旋转的性质、勾股定理可得![]() ,
,![]() ,然后根据直角三角形的面积公式可得S与x的函数关系式,最后利用二次函数的解析式即可得点P的坐标;
,然后根据直角三角形的面积公式可得S与x的函数关系式,最后利用二次函数的解析式即可得点P的坐标;
(3)先根据旋转的性质、正方形的性质得出![]() ,
,![]() ,从而得出点P在OB的延长线上,再根据线段的和差可得
,从而得出点P在OB的延长线上,再根据线段的和差可得![]() ,然后同(1)的方法可得
,然后同(1)的方法可得![]() ,
,![]() ,最后根据三角形全等的性质、线段的和差可得
,最后根据三角形全等的性质、线段的和差可得![]() ,由此即可得出答案.
,由此即可得出答案.
(1)如图1,过P点作![]() 轴于点G,过Q点作
轴于点G,过Q点作![]() 轴于点H
轴于点H
∵四边形OABC是正方形
∴![]()
∵![]()
∴![]()
在![]() 中,
中,![]() ,
,![]()
∴![]()
∵![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 得到
得到![]()
∴![]() ,
,![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
∴![]()
∴![]()
∴![]()
则点Q的坐标为![]() ;
;
(2)如图2,过P点作![]() 轴于点G
轴于点G
∵![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 得到
得到![]()
∴![]()
∵![]()
∴![]() ,
,![]()
∴![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
整理得:![]()
∴![]()
整理得:![]()
![]()
![]() 由二次函数的性质可知,当
由二次函数的性质可知,当![]() 时,S随x的增大而减小;当
时,S随x的增大而减小;当![]() 时,S随x的增大而增大
时,S随x的增大而增大
则当![]() 时,S取得最小值,最小值为9
时,S取得最小值,最小值为9
此时![]()
故点P的坐标为![]() ;
;
(3)∵![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() 得到
得到![]()
∴![]()
∵![]()
∴![]()
∵四边形OABC是正方形,且边长![]()
![]() 对角线
对角线![]()
∴点P在OB的延长线上
∴![]()
解得![]()
![]()
如图3,过P点作![]() 轴于点G,过Q点作
轴于点G,过Q点作![]() 轴于点H
轴于点H
同(1)可得:![]() ,
,![]()
![]() ,
,![]()
![]()
则点Q的坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则小明打开走廊灯的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
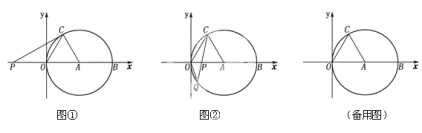
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组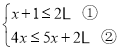 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(1)解不等式①,得_________________;
(2)解不等式②,得_________________;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
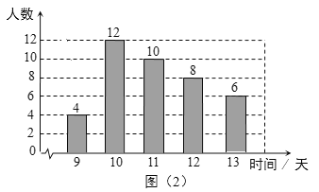
【题目】学校为了解全校学生参加社会实践活动情况,随机调查了部分学生一学期参加社会实践活动的时间(单位:天),并用得到的数据绘制了统计图(1)和图 (2). 请根据图中提供的信息,回答下列问题:

![]()
(1) 本次随机调查的学生人数是_______,图(1)中m的值是_______;
(2)求调查获取的学生社会实践活动时间样本数据的众数、中位数和平均数;
(3)该校有480名学生,根据获取的社会实践活动时间样本数据,估计该校一学期社会实践活动时间大于10 天的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
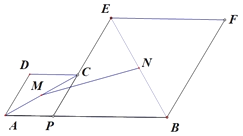
【题目】如图,已知![]() ,
,![]() 为线段
为线段![]() 上的一个动点,分别以
上的一个动点,分别以![]() ,
,![]() 为边在
为边在![]() 的同侧作菱形
的同侧作菱形![]() 和菱形
和菱形![]() ,点
,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() .
.![]() ,
,![]() 分别是对角线
分别是对角线![]() ,
,![]() 的中点.当点
的中点.当点![]() 在线段
在线段![]() 上移动时,点
上移动时,点![]() ,
,![]() 之间的距离最短为( )
之间的距离最短为( )
A.![]() B.
B.![]() C.4D.3
C.4D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,并开设了跳绳、足球、篮球、跑步四种运动项目,为了解学生最喜爱哪一种项目,随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出).
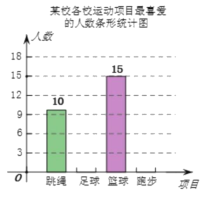
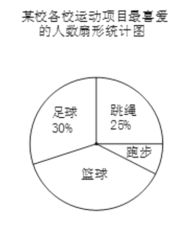
(1)求本次被调查的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,“篮球”部分所对应的圆心角度数为__ ;
(4)该校共有3000名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
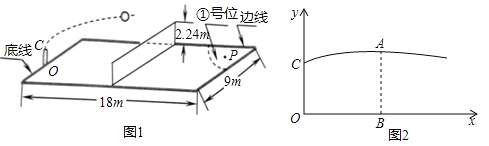
【题目】如图1,排球场长为18m,宽为9m,网高为2.24m.队员站在底线O点处发球,球从点O的正上方1.9m的C点发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m.即BA=2.88m.这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2.
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围).并判断这次发球能否过网?是否出界?说明理由;
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m,边线0.5m),问发球点O在底线上的哪个位置?(参考数据:![]() 取1.4)
取1.4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com