
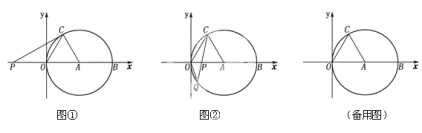
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
【答案】(1)60°.(2)4.(3)2或2+2![]() .
.
【解析】
试题(1)OA=AC首先三角形OAC是个等腰三角形,因为∠AOC=60°,三角形AOC是个等边三角形,因此∠OAC=60°;
(2)如果PC与圆A相切,那么AC⊥PC,在直角三角形APC中,有∠PCA的度数,有A点的坐标也就有了AC的长,可根据余弦函数求出PA的长,然后由PO=PA-OA得出OP的值.
(3)本题分两种情况:
①以O为顶点,OC,OQ为腰.那么可过C作x轴的垂线,交圆于Q,此时三角形OCQ就是此类情况所说的等腰三角形;那么此时PO可在直角三角形OCP中,根据∠COA的度数,和OC即半径的长求出PO.
②以Q为顶点,QC,QD为腰,那么可做OC的垂直平分线交圆于Q,则这条线必过圆心,如果设垂直平分线交OC于D的话,可在直角三角形AOQ中根据∠QAE的度数和半径的长求出Q的坐标;然后用待定系数法求出CQ所在直线的解析式,得出这条直线与x轴的交点,也就求出了PO的值.
试题解析:(1)∵∠AOC=60°,AO=AC,
∴△AOC是等边三角形,
∴∠OAC=60°.
(2)∵CP与A相切,
∴∠ACP=90°,
∴∠APC=90°-∠OAC=30°;
又∵A(4,0),
∴AC=AO=4,
∴PA=2AC=8,
∴PO=PA-OA=8-4=4.
(3)①过点C作CP1⊥OB,垂足为P1,延长CP1交⊙A于Q1;
∵OA是半径,
∴ 弧OC=弧OQ1,
∴OC=OQ1,
∴△OCQ1是等腰三角形;
又∵△AOC是等边三角形,
∴P1O=![]() OA=2;
OA=2;
②过A作AD⊥OC,垂足为D,延长DA交⊙A于Q2,CQ2与x轴交于P2;
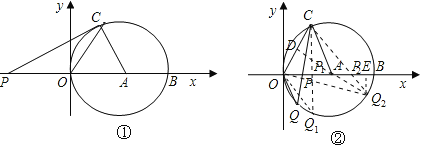
∵A是圆心,
∴DQ2是OC的垂直平分线,
∴CQ2=OQ2,
∴△OCQ2是等腰三角形;
过点Q2作Q2E⊥x轴于E,
在Rt△AQ2E中,
∵∠Q2AE=∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∴Q2E=![]() AQ2=2,AE=2
AQ2=2,AE=2![]() ,
,
∴点Q2的坐标(4+2![]() ,-2);
,-2);
在Rt△COP1中,
∵P1O=2,∠AOC=60°,
∴CP1=2![]() ,
,
∴C点坐标(2,2![]() );
);
设直线CQ2的关系式为y=kx+b,则
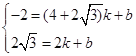 ,解得
,解得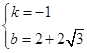 ,
,
∴y=-x+2+2![]() ;
;
当y=0时,x=2+2![]() ,
,
∴P2O=2+2![]() .
.
考点: 1.切线的性质;2.等腰三角形的性质;3.等边三角形的性质.


科目:初中数学 来源: 题型:
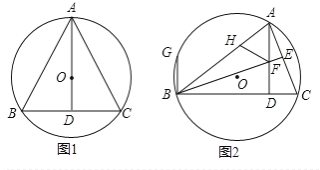
【题目】已知锐角△ABC内接于O,AD⊥BC.垂足为D.
(1)如图1,若![]() ,BD=DC,求∠B的度数.
,BD=DC,求∠B的度数.
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG;
①连接CG,试探究∠ABC,∠ACG的数量关系,并给予证明.
②求证:△AFH是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,3为半径作圆.试判断:
①点C与⊙A的位置关系;②点B与⊙A的位置关系;③AB中的D点与⊙A的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
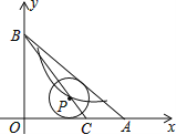
【题目】如图,在Rt△OAB中,OA=4,AB=5,点C在OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数![]() (k≠0)的图象经过圆心P,则k=________________。
(k≠0)的图象经过圆心P,则k=________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张正面分别标有数字![]() 的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为![]() ,另有一个被均匀分成4份的转盘,上面分别标有数字
,另有一个被均匀分成4份的转盘,上面分别标有数字![]() ,转动转盘,指针所指的数字记为
,转动转盘,指针所指的数字记为![]() (若指针指在分割线上则重新转一次),则点
(若指针指在分割线上则重新转一次),则点![]() 落在抛物线
落在抛物线![]() 与
与![]() 轴所围成的区域内(不含边界)的概率是__________.
轴所围成的区域内(不含边界)的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
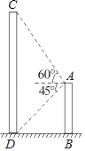
【题目】如图,两幢大楼AB,CD之间的水平距离(BD)为20米,为测得两幢大楼的高度,小王同学站在大楼AB的顶端A处测得大楼CD顶端C的仰角为60°,测得大楼CD的底部D的俯角为45°,试求大楼AB和CD的高度.(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的顶点M在第二象限,且经过点 A(1,0)和点 B(0,2).则
(1)a 的取值范围是________;
(2)若△AMO的面积为△ABO面积的![]() 倍时,则a的值为________
倍时,则a的值为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com