
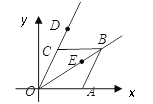
【题目】如图,菱形OABC中,点A在x轴上,顶点C的坐标为(1,![]() ),动点D、E分别在射线OC、OB上,则CE+DE+DB的最小值是____.
),动点D、E分别在射线OC、OB上,则CE+DE+DB的最小值是____.
【答案】4
【解析】
连接AC,作B关于直线OC的对称点![]() ,连接
,连接![]() 交OC于点D,交OB于点E,此时CE+DE+BD的值最小,结合题意求出CE+DE+DB=
交OC于点D,交OB于点E,此时CE+DE+BD的值最小,结合题意求出CE+DE+DB=![]() ,然后,再过点C作CN⊥OA于N点,进一步得出∠
,然后,再过点C作CN⊥OA于N点,进一步得出∠![]() =90°,
=90°,![]() =BF=
=BF=![]() 以及AB=2,最后根据勾股定理求出答案即可.
以及AB=2,最后根据勾股定理求出答案即可.

如图,连接AC,作B关于直线OC的对称点![]() ,连接
,连接![]() 交OC于点D,交OB于点E,此时CE+DE+BD的值最小,
交OC于点D,交OB于点E,此时CE+DE+BD的值最小,
∵四边形OCBA为菱形,
∴AC⊥OB,AO=OC,
即点A与点C关于OB对称,
∴CE=AE,
∴DE+CE=DE+AE=AD,
∵点B与点![]() 关于OC对称,
关于OC对称,
∴![]() ,
,
∴CE+DE+DB=AD+![]() =
=![]() ,
,
此时,过点C作CN⊥OA于N点,
∵C点坐标为(1,![]() ),
),
∴ON=1,CN=![]() ,
,
由勾股定理可得:OC=2,
即AB=BC=OA=OC=2,
∴∠CON=60°,
∵四边形COBA为菱形,
∴∠CBA=∠COA=60°,BC∥OA,
∴∠DCB=∠COA=60°,
∵点B与点![]() 关于OC对称,
关于OC对称,
∴∠BFC=90°,![]() ,
,
∴∠![]() =30°,
=30°,
∴∠![]() =30°+60°=90°,CF=
=30°+60°=90°,CF=![]() BC=1,
BC=1,
由勾股定理可得:BF=![]() ,
,
∴![]() ,
,
在Rt△![]() 中,
中,![]() ,
,
∴CE+DE+DB的最小值为4,
故答案为:4.


科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有3个球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个球是白球的概率;
(2)摸出1个球,记下颜色后放回,并搅均,再摸出1个球.求两次摸出的球恰好颜色不同的概率(要求画树状图或列表);
(3)现再将n个白球放入布袋,搅均后,使摸出1个球是白球的概率为![]() .求n的值.
.求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,图中四个直角三角形是全等的,若大正方形ABCD的面积是小正方形EFGH面积的13倍,则![]() 的值为______________.
的值为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,过点D作⊙O的切线,与边BC交于点E,若AD=![]() , AC=3.则DE长为( )
, AC=3.则DE长为( )
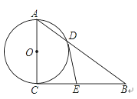
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程
(1)x2﹣4x+1=0 (2)(5x﹣3)2+2(3﹣5x)=0
(3)(2x+1)2=(x﹣1)2 (4)4x2+2=7x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
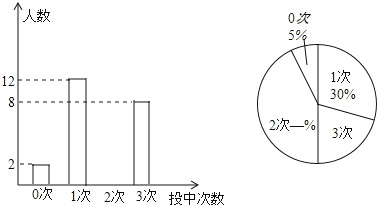
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
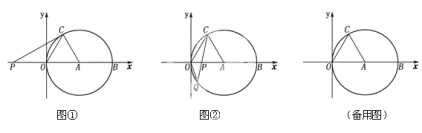
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com