练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，菱形ABOC的AB，AC分别与⊙O相切于点D、E，若点D是AB的中点，则∠DOE=__________.

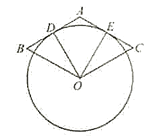
    【答案】60°

    【解析】由AB，AC分别与⊙O相切于点D、E，可得∠BDO=∠ADO=∠AEO=90°，根据已知条件可得到BD=OB，在Rt△OBD中，求得∠B=60°，继而可得∠A=120°，再利用四边形的内角和即可求得∠DOE的度数.

    【详解 】∵AB，AC分别与⊙O相切于点D、E，

    ∴∠BDO=∠ADO=∠AEO=90°，

    ∵四边形ABOC是菱形，∴AB=BO，∠A+∠B=180°，

    ∵BD=AB，

    ∴BD=OB，

    在Rt△OBD中，∠ODB=90°，BD=OB，∴cos∠B=，∴∠B=60°，

    ∴∠A=120°，

    ∴∠DOE=360°-120°-90°-90°=60°，

    故答案为：60°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，∠D＝15°，则∠A＝__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下表:

    我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y，第 2 格的“特征多项式”为 8x+4y, 回答下列问题:

    (1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .

    (2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若 x 满足 (9x)(x4)=4， 求 (4x)2+(x9)2 的值.

    设 9x=a，x4=b， 则 (9x)(x4)=ab=4，a+b=(9x)+(x4)=5 ，

    ∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13

    请仿照上面的方法求解下面问题：

    (1)若 x 满足 (5x)(x2)=2， 求 (5x)2+(x2)2 的值

    (2)已知正方形 ABCD 的边长为 x ， E ， F 分别是 AD 、 DC 上的点，且 AE=1 ， CF=3 ，长方形 EMFD 的面积是 48 ，分别以 MF 、 DF 作正方形，求阴影部分的面积.

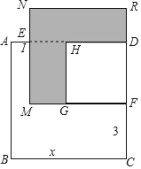
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，二次函数的图象与x轴交于A、B两点，B点的坐标为(3，0)，与y轴交于点C（0，－3），点P是直线BC下方抛物线上的一个动点．

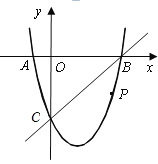
    （1）求二次函数解析式；

    （2）连接PO，PC，并将△POC沿y轴对折，得到四边形.是否存在点P，使四边形为菱形？若存在，求出此时点P的坐标；若不存在，请说明理由；

    （3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知点O，A，B均为网格线的交点.

    （1）在给定的网格中，以点O为位似中心，将线段AB放大为原来的2倍，得到线段（点A，B的对应点分别为）.画出线段;

    （2）将线段绕点逆时针旋转90°得到线段.画出线段;

    （3）以为顶点的四边形的面积是 个平方单位.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明大学毕业回家乡创业，第一期培植盆景与花卉各50盆售后统计，盆景的平均每盆利润是160元，花卉的平均每盆利润是19元，调研发现：

    ①盆景每增加1盆，盆景的平均每盆利润减少2元;每减少1盆，盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.

    小明计划第二期培植盆景与花卉共100盆，设培植的盆景比第一期增加x盆，第二期盆景与花卉售完后的利润分别为W1，W2（单位：元）

    （1）用含x的代数式分别表示W1，W2;

    （2）当x取何值时，第二期培植的盆景与花卉售完后获得的总利润W最大，最大总利润是多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F.

    (1)求证：DF⊥AC；

    (2)若⊙O的半径为5，∠CDF=30°，求的长(结果保留π)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点为直线上一点，过点作射线，使将一直角三角板的直角顶点放在点处，一边在射线上，另一边在直线的下方．

    （1）将图1中的三角形板绕点按照顺时针方向旋转至图2的位置，使得落在射线上，此时旋转的角度是____°；

    （2）继续将图2中的三角板绕点按顺时针方向旋转至图3的位置，使得在的内部，则_____________°；

    （3）在上述直角板从图1旋转到图3的位置的过程中，若三角板绕点按每秒钟的速度旋转，当恰好为的平分线时，此时，三角板绕点运动时间为__秒，并说明理由．

    查看答案和解析>>

    同步练习册答案