
【题目】观察下表:

我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y,第 2 格的“特征多项式”为 8x+4y, 回答下列问题:
(1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .
(2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.
【答案】(1)12x+9y,16x+16y,4nx+n2y;(2)24x+36y.
【解析】
(1)根据表格中的数据找出规律即可解答本题;
(2)根据(1)中的结果可以写出第m格的“特征多项式”,然后根据“和不含有x项”可以求得m的值,从而可以写出此“特征多项式”.
解:(1)由表格可得:第3格的“特征多项式”为12x+9y,第4格的“特征多项式”为16x+16y,第n格的“特征多项式”为4nx+n2y,
故答案为:12x+9y,16x+16y,4nx+n2y;
(2)由(1)可得,第m格的“特征多项式”是4mx+m2y,
∴(4mx+m2y)+(24x+2y5)=4mx+m2y24x+2y5=(4m24)x+(m2+2)y5,
∵第m格的“特征多项式”与多项式24x+2y5的和不含有x项,
∴4m24=0,解得m=6,
∴此“特征多项式”是24x+36y.


科目:初中数学 来源: 题型:
【题目】已知A=2x2﹣6ax+3,B=﹣7x2﹣8x﹣1,按要求完成下列各小题.
(1)若A+B的结果中不存在含x的一次项,求a的值;
(2)当a=﹣2时,求A﹣3B的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
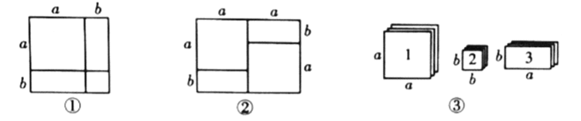
某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如,图①可以解释![]() ,因此,我们可以利用这种方法对某些多项式进行因式分解.
,因此,我们可以利用这种方法对某些多项式进行因式分解.
根据阅读材料回答下列问题:
(1)如图②所表示的因式分解的恒等式是________________________.
(2)现有足够多的正方形和长方形卡片(如图③),试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形(每两张卡片之间既不重叠,也无空隙),使该长方形的面积为![]() ,并利用你画的长方形的面积对
,并利用你画的长方形的面积对![]() 进行因式分解.
进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
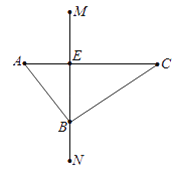
【题目】如图,南北向MN为我国领海线,即MN以西为我国领海,以东为公海,上午9时50分,我国反走私A艇发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来,便立即通知正在MN线上巡逻的我国反走私艇B密切注意.反走私艇A和走私艇C的距离是13海里,A、B两艇的距离是5海里;反走私艇B测得距离C艇12海里,若走私艇C的速度不变,最早会在什么时候进入我国领海?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点C是线段AB的中点
(1)如图,若点D在线段CB上,且BD=1.5厘米,AD=6.5厘米,求线段CD的长度;
![]()
(2)若将(1)中的“点D在线段CB上”改为“点D在线段CB的延长线上”,其他条件不变,请画出相应的示意图,并求出此时线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
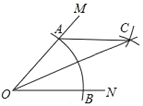
【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为![]() .求:(1)求BF+CE的值; (2)求△ABC的周长.
.求:(1)求BF+CE的值; (2)求△ABC的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com