
【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.
【答案】(1)、15米;(2)、t=2+![]() 或t=2-
或t=2-![]() ;(3)、0≤m<20
;(3)、0≤m<20
【解析】
试题分析:(1)、将t=3代入解析式可得;(2)、根据h=10可得关于t的一元二次方程,解方程即可;(3)、由题意可得方程20t﹣t2=m 的两个不相等的实数根,由根的判别式即可得m的范围.
试题解析:(1)、当t=3时,h=20t﹣5t2=20×3﹣5×9=15(米),
∴当t=3时,足球距离地面的高度为15米;
(2)、∵h=10, ∴20t﹣5t2=10,即t2﹣4t+2=0, 解得:t=2+![]() 或t=2﹣
或t=2﹣![]() ,
,
故经过2+![]() 或2﹣
或2﹣![]() 时,足球距离地面的高度为10米;
时,足球距离地面的高度为10米;
(3)、∵m≥0,由题意得t1,t2是方程20t﹣5t2=m 的两个不相等的实数根,
∴b2﹣4ac=202﹣20m>0, ∴m<20, 故m的取值范围是0≤m<20.


科目:初中数学 来源: 题型:
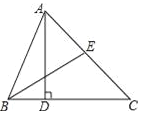
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=70°.
(1)求∠CAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为
查看答案和解析>>
科目:初中数学 来源: 题型:
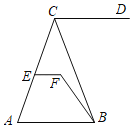
【题目】如图,EF∥AB,∠DCB=65°,∠CBF=15°,∠EFB=130°.
(1)直线CD与AB平行吗?为什么?
(2)若∠CEF=68°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某动物园在![]() 天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
人数变化 (单位:万人) | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)若![]() 月
月![]() 日的游客人数记为
日的游客人数记为![]() 万人,请用含
万人,请用含![]() 的代数式表示
的代数式表示![]() 月
月![]() 日的游客人数,并直接写出七天内游客人数最多的是哪一天?
日的游客人数,并直接写出七天内游客人数最多的是哪一天?
(2)若![]() 月
月![]() 日的游客人数为
日的游客人数为![]() 万人,门票每人
万人,门票每人![]() 元,问黄金周期间该动物园门票总收入是多少万元?
元,问黄金周期间该动物园门票总收入是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表:

我们把表格中字母的和所得的多项式称为"'特征多项式",例如:第1格的“特征多项式”为 4x+y,第 2 格的“特征多项式”为 8x+4y, 回答下列问题:
(1)第 3 格的“特征多项式”为 第 4 格的“待征多项式”为 , 第 n 格的“特征多项式”为 .
(2)若第 m 格的“特征多项式”与多项式-24x+2y-5 的和不含有 x 项,求此“特征多项式”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+![]() =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
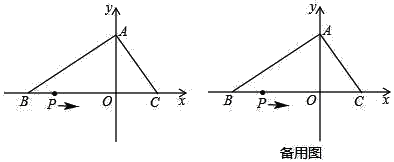
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
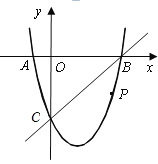
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
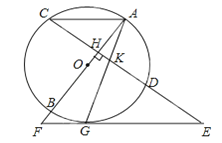
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com