练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

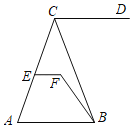
    【题目】如图，EF∥AB，∠DCB＝65°，∠CBF＝15°，∠EFB＝130°．

    （1）直线CD与AB平行吗？为什么？

    （2）若∠CEF＝68°，求∠ACB的度数．

    【答案】（1）CD与AB平行，见解析；（2）47°

    【解析】

    （1）根据两直线平行、同旁内角互补求出∠ABF，得到∠ABC，根据内错角相等、两直线平行证明；

    （2）根据两直线平行、同旁内角互补求出∠DCE，计算即可．

    （1）CD与AB平行，理由如下：

    ∵EF∥AB，

    ∴∠EFB+∠ABF＝180°，

    ∴∠ABF＝180°﹣130°＝50°，

    ∴∠ABC＝∠ABF+∠CBF＝65°，

    ∴∠ABC＝∠DCB，

    ∴CD∥AB；

    （2）∵CD∥EF，

    ∴∠DCE+∠CEF＝180°，

    ∴∠DCE＝180°﹣68°＝112°，

    ∴∠ACB＝∠DCE﹣∠DCB＝47°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某剧院的观众席的座位为扇形，且按下列分式设置：

    排数（x）

    1

    2

    3

    4

    …

    座位数（y）

    50

    53

    56

    59

    …

    （1）按照上表所示的规律，当x每增加1时，y如何变化？

    （2）写出座位数y与排数x之间的关系式；

    （3）按照上表所示的规律，某一排可能有90个座位吗？说说你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料阅读

    角是一种基本的几何图像，如图1角可以看作由一条射线绕着它的端点旋转而形成的图形．钟面上的时针与分针给我们以角的形象．如果把图2作为钟表的起始状态，对于一个任意时刻时针与分针的夹角度数可以用下面的方法确定．

    因为时针绕钟面转一圈（）需要12小时，所以时针每小时转过．

    如图3中时针就转过．

    因为分针绕钟面转一圈（）需要60分钟，所以分针每分钟转过．

    如图4中分针就转过．

    再如图5中时针转过的度数为，分针转过的度数记为，此时，分针转过的度数大于时针转过的度数，所以时针与分针的夹角为．

    知识应用

    请使用上述方法，求出时针与分针的夹角．

    拓广探索

    张老师某周六上午7点多去菜市场买菜，走时发现家中钟表时钟与分针的夹角是直角，买菜回到家发现钟表时针与分针的夹角还是直角，可以确定的是张老师家的钟表没有故障，走时正常，且回家时间还没到上午8点，请利用上述材料所建立数学模型列方程，求出张老师约7点多少分出门买菜？约7点多少分回到家？（结果用四舍五入法精确到分．）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图 1，两个完全相同的三角形纸片 ABC 和 DEC 重合放置，其中∠C=90°，∠B=∠E=30°．

    ⑴ 操作发现：如图 2，固定△ABC，使△DEC 绕点 C 旋转，当点 D 恰好落在 AB 边上时， 填空：

    ①线段 DE 与 AC 的位置关系是 ；

    ②设△BDC 的面积为 S1，△AEC 的面积为 S2，则 S1 与 S2 的数量关系是 ．

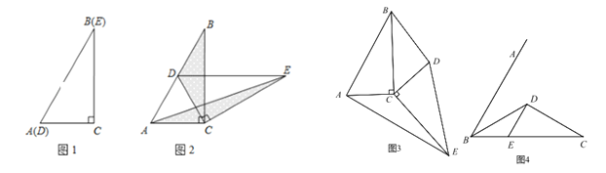
    ⑵ 猜想论证

    当△DEC 绕点 C 旋转到如图 3 所示的位置时，请猜想（1）中 S1 与 S2 的数量关系是否仍 然成立？若成立，请证明；若不成立，请说明理由．

    ⑶ 拓展探究

    已知∠ABC=60°，BD 平分∠ABC，BD=CD，BE=6，DE∥AB 交 BC 于点 E（如图 4）．若在射线 BA 上存在点 F，使 S△DCF=S△BDE，请求相应的 BF 的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如右上图，在正方形ABCD中AB=3，，以B为圆心，半径为1画⊙B，点P在⊙B上移动，连接AP，并将AP绕点A逆时针方向旋转 90°至AP′，连接BP′，在点P移动过程中，BP′长的取值范围是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    某些代数恒等式可用一些卡片拼成的图形的面积来解释.例如，图①可以解释，因此，我们可以利用这种方法对某些多项式进行因式分解.

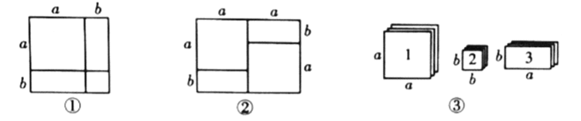
    根据阅读材料回答下列问题：

    （1）如图②所表示的因式分解的恒等式是________________________.

    （2）现有足够多的正方形和长方形卡片（如图③），试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的长方形（每两张卡片之间既不重叠，也无空隙），使该长方形的面积为，并利用你画的长方形的面积对进行因式分解.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于抛物线y＝－x2＋2x＋3，有下列四个结论：①它的对称轴为x＝1；

    ②它的顶点坐标为(1，4)；

    ③它与y轴的交点坐标为(0，3)，与x轴的交点坐标为(－1，0)和(3，0)；

    ④当x＞0时，y随x的增大而减小．

    其中正确的个数为(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把一个足球垂直水平地面向上踢，时间为t（秒）时该足球距离地面的高度h（米）适用公式h=20t﹣5t2（0≤t≤4）．

    （1）当t=3时，求足球距离地面的高度；

    （2）当足球距离地面的高度为10米时，求t；

    （3）若存在实数t1，t2（t1≠t2）当t=t1或t2时，足球距离地面的高度都为m（米），求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】自行车厂某周计划生产2100辆电动车，平均每天生产电动车300辆．由于各种原因，实际每天的生产量与计划每天的生产量相比有出入，下表是该周的实际生产情况(超产记为正、减产记为负，单位：辆)：

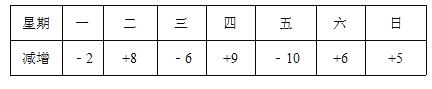
    （1）该厂星期一生产电动车　　　　 辆；

    （2）生产量最多的一天比生产量最少的一天多生产电动车　　　　 辆；

    （3）该厂实行记件工资制，每生产一辆车可得60元，那么该厂工人这一周的工资总额是多少元？

    查看答案和解析>>

    同步练习册答案