
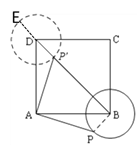
【题目】如右上图,在正方形ABCD中AB=3,,以B为圆心,半径为1画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针方向旋转 90°至AP′,连接BP′,在点P移动过程中,BP′长的取值范围是______.

【答案】3![]() -1≤BP′≤3
-1≤BP′≤3![]() +1
+1
【解析】通过画图发现,点P'的运动路线为以D为圆心,以1为半径的圆,可知:当P'在对角线BD上时,![]() 最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出
最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出![]() 的长,而最长距离则是最短距离加上圆的直径即可.
的长,而最长距离则是最短距离加上圆的直径即可.
如图,当P′在对角线BD上时,BP′最小,连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=![]() ,
,
∴BP′=BD-P′D=3![]() -1,BE=3
-1,BE=3![]() -1+2=3
-1+2=3![]() +1,
+1,
即BP′长度的最小值为(3![]() -1)cm,最长距离为:3
-1)cm,最长距离为:3![]() +1.
+1.
故答案为:3![]() -1≤BP′≤3
-1≤BP′≤3![]() +1.
+1.


科目:初中数学 来源: 题型:
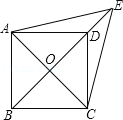
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,小东测得一根长为1 m的竹竿的影长为0.4 m.
(1)求同一时刻2 m的竹竿的影长;
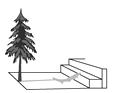
(2)同一时刻小东在测量树的高度时,发现树的影子不全落在地面上,有一部分落在操场的第一级台阶上,如图,测得落在第一级台阶上的影子长为0.1 m,第一级台阶的高为0.3 m,落在地面上的影子长为4.3 m,求树的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
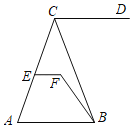
【题目】如图,EF∥AB,∠DCB=65°,∠CBF=15°,∠EFB=130°.
(1)直线CD与AB平行吗?为什么?
(2)若∠CEF=68°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶![]() ,先到终点的人原地休息.已知甲先出发
,先到终点的人原地休息.已知甲先出发![]() ,在整个过程中,甲、乙两车的距离
,在整个过程中,甲、乙两车的距离![]() 与甲出发的时间
与甲出发的时间![]() 之间的关系如图所示.
之间的关系如图所示.
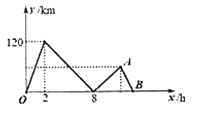
(1)甲的速度为______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)说明![]() 点表示的意义,求出
点表示的意义,求出![]() 点坐标;
点坐标;
(3)求出线段![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)甲出发多长时间两车相距![]() ,直接写出结果.
,直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com