
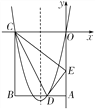
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

【答案】⑴![]() ⑵存在AP=
⑵存在AP=![]() ⑶ 存在,∠PBQ=45°
⑶ 存在,∠PBQ=45°
【解析】(1)根据∠PBC+∠ABP=∠ABP+∠APB=90°得出∠APB=∠PBC ,再由tan∠PBC=tan∠APB=4=![]() ;(2) 延长PQ交BC延长线于点E.设PD=x,由 ∠PBC=∠BPQ ,可得EB=EP ,再由△PDQ≌△ECQ 得到QP=
;(2) 延长PQ交BC延长线于点E.设PD=x,由 ∠PBC=∠BPQ ,可得EB=EP ,再由△PDQ≌△ECQ 得到QP=![]() ,在Rt△PDQ中根据勾股定理可得出结论;(3) 作BH⊥PQ于
,在Rt△PDQ中根据勾股定理可得出结论;(3) 作BH⊥PQ于![]() 点,易证,△PAB≌△PHB,可得∠PBH=
点,易证,△PAB≌△PHB,可得∠PBH=![]() ∠ABH,再由 Rt△BHQ≌Rt△BCQ,可得∠HBQ=
∠ABH,再由 Rt△BHQ≌Rt△BCQ,可得∠HBQ=![]() ∠HBC,进而得出结论即可.
∠HBC,进而得出结论即可.
(1)∵∠PBC+∠ABP=∠ABP+∠APB=90°, ∴∠APB=∠PBC=90°,在RT△ABP中,tan∠PBC=tan∠APB=4=![]() ;
;
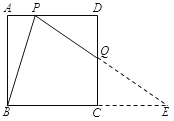
⑵如图1,存在![]()
延长PQ交BC延长线于点E.设PD=x.
∵∠PBC=∠BPQ,
∴EB=EP.
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DPQ=∠E,.
在△PDQ和△ECQ中,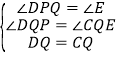 ,
,
∴△PDQ≌△ECQ(AAS).
∴PD=CE,PQ=QE. ∴BE=EP=![]() , ∴QP=
, ∴QP=![]() .
.
在Rt△PDQ中,∵PD2+QD2=PQ2,
∴![]() ,解得
,解得![]()
∴AP=AD﹣PD=![]() .
.
⑶存在,∠PBQ=45°.作![]() 于
于![]() 点.
点.
易证,△PAB≌△PHB,
∴∠ABP=∠HBP, ∴∠PBH=![]() ∠ABH.
∠ABH.
易证,Rt△BHQ≌Rt△BCQ,
∴∠HBQ=∠CBQ, ∴∠HBQ=![]() ∠HBC,
∠HBC,
∴∠PBQ=∠PBH+∠HBQ=![]() (∠ABH+∠HBC)=
(∠ABH+∠HBC)=![]() ∠ABC=45°.
∠ABC=45°.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是

A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.已知数轴上有点A和点B,点A和点B分别表示数-20和40,请解决以下问题:
(1)请画出数轴,并标明A、B两点;
(2)若点P、Q分别从点A、点B同时出发,相向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点C时,C所对应的数是多少?
(3)若点P、Q分别从点A、点B同时出发,沿x轴正方向同向而行,点P、Q移动的速度分别为每秒4个单位长度和2个单位长度.问:当P、Q相遇于点D时,D所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右上图,在正方形ABCD中AB=3,,以B为圆心,半径为1画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针方向旋转 90°至AP′,连接BP′,在点P移动过程中,BP′长的取值范围是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的位置如图所示(每个小方格都是边长1个单位长度的正方形).
的位置如图所示(每个小方格都是边长1个单位长度的正方形).
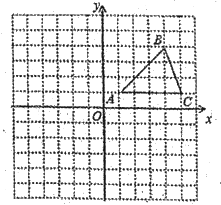
(1)将![]() 沿
沿![]() 轴方向向左平移6个单位,画出平移后得到的
轴方向向左平移6个单位,画出平移后得到的![]() .
.
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;直接写出点
;直接写出点![]() 的坐标.
的坐标.
(3)作出![]() 关于原点
关于原点![]() 成中心对称的
成中心对称的![]() ,并直接写出
,并直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=-x2+2x+3,有下列四个结论:①它的对称轴为x=1;
②它的顶点坐标为(1,4);
③它与y轴的交点坐标为(0,3),与x轴的交点坐标为(-1,0)和(3,0);
④当x>0时,y随x的增大而减小.
其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),其对称轴为直线x=1,下列结论中正确的是( )
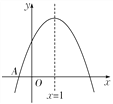
A. abc>0 B. 2a-b=0 C. 4a+2b+c<0 D. 9a+3b+c=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的表达式;
(3)一动点P从点C 出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E 点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t s,当t为何值时,DP=DQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com