
【题目】如图,在矩形OABC 中,OA=5,AB=4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA边上的点E 处,分别以OC,OA 所在的直线为x 轴,y 轴建立平面直角坐标系.
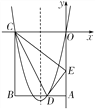
(1)求OE 的长;
(2)求经过O,D,C 三点的抛物线的表达式;
(3)一动点P从点C 出发,沿CB以每秒2 个单位长的速度向点B运动,同时动点Q从E 点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t s,当t为何值时,DP=DQ.
【答案】(1)3(2) y=![]() x2+
x2+![]() x;(3)
x;(3)![]()
【解析】
(1)在Rt△COE中,OE=![]() ;
;
(2)在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m,求得:O,D,C的坐标,再代入解析式,可解得;
(3)由CP=2t,BP=5-2t,和BD=DE=![]() ,再证Rt△DBP≌Rt△DEQ,得BP=EQ.可求得t.
,再证Rt△DBP≌Rt△DEQ,得BP=EQ.可求得t.
解:(1)∵CE=CB=5,CO=AB=4,
∴在Rt△COE中,
OE=![]() =3;
=3;
(2)设AD=m,则DE=BD=4-m,
∵OE=3,∴AE=5-3=2,
在Rt△ADE中,由勾股定理可得AD2+AE2=DE2,即m2+22=(4-m)2,解得m=![]() ,
,
∴D![]() ,∵C(-4,0),O(0,0),
,∵C(-4,0),O(0,0),
∴设过O,D,C三点的抛物线为y=ax(x+4),
∴-5=![]() ,解得a=
,解得a=![]() ,
,
∴抛物线表达式为y=![]() x(x+4)=
x(x+4)=![]() x2+
x2+![]() x;
x;
(3)∵CP=2t,∴BP=5-2t,
由折叠的性质,得BD=DE=![]() ,
,
在Rt△DBP和Rt△DEQ中,![]() ,
,
∴Rt△DBP≌Rt△DEQ(HL)
∴BP=EQ,
∴5-2t=t,∴t=![]() .
.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
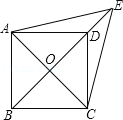
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】① 如图(1),直线l上有2个点,则图中有2条可用图中字母表示的射线:A1A2、A2A1,有1条线段:A1A2;
② 如图(2),直线l上有3个点,则图中有几条可用图中字母表示的射线,有几条线段,并分别用图中字母表示出来;
③ 如图(3),直线l上有n个点,则图中有多少条可用图中字母表示的射线,有多少条线段,分别用含n的代数式表示出来;
④ 应用(3)中发现的规律解决问题:某校七年级共有8个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需多少场比赛?
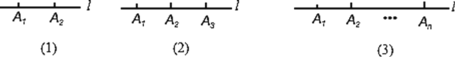
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+![]() =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
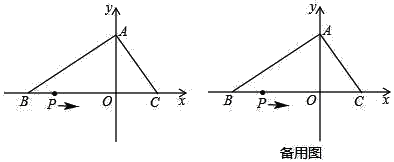
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润____元;
(2)若设后来该小商品每件降价x元,该经营者一天可获利润y元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y与x之间的函数关系式,并求出当x取何值时,该经营者所获利润最大,且最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶![]() ,先到终点的人原地休息.已知甲先出发
,先到终点的人原地休息.已知甲先出发![]() ,在整个过程中,甲、乙两车的距离
,在整个过程中,甲、乙两车的距离![]() 与甲出发的时间
与甲出发的时间![]() 之间的关系如图所示.
之间的关系如图所示.
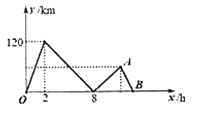
(1)甲的速度为______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)说明![]() 点表示的意义,求出
点表示的意义,求出![]() 点坐标;
点坐标;
(3)求出线段![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)甲出发多长时间两车相距![]() ,直接写出结果.
,直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
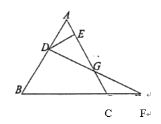
【题目】如图,在边长为1的等边△ABC的边AB取一点D,过点D作DE⊥AC于点E,在BC延长线取一点F,使CF=AD,连接DF交AC于点G,则EG的长为________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com