
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是

A.①②B.①④C.②③D.②④
 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】已知线段![]() 和线段
和线段![]() .
.

(1)按要求作图(保留作围痕迹,不写作法);
延长线段![]() 至点
至点![]() ,使
,使![]() ,反向延长线段
,反向延长线段![]() 至点
至点![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,且
的中点,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,且点
,且点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
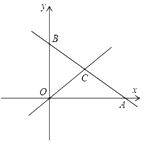
(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)直线![]() 上有一点
上有一点![]() ,若
,若![]() ,试求出点
,试求出点![]() 的坐标;
的坐标;
(3)若点![]() 为直线
为直线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
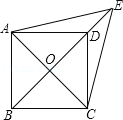
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,点P是边AD上的动点(点P不与点A、点D重合),点Q是边CD上一点,连接PB、PQ,且∠PBC=∠BPQ.
⑴ 若tan∠PBC=4,求AP的长;
⑵ 是否存在点P,使得点Q恰好是边CD的中点?若存在,求出AP的长;若不存在,请说明理由.⑶ 连接BQ,在△PBQ中是否存在度数不变的角?若存在,指出这个角,并求出它的度数;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com