
����Ŀ��������˾Ϊ���������Լ�õ磬��ȡ�����õ����ֶ��շѰ취����ij������ÿ��Ӧ�����y��Ԫ�����õ���x���ȣ��ĺ���ͼ����һ�����ߣ���ͼ��ʾ��������ͼ����������⣺
(1) �ֱ�д����0��x��100��x��100ʱ��y��x�ĺ�����ϵʽ
(2) ���ú�����ϵʽ��˵��������˾��ȡ���շѱ�
(3) �����û�ij���õ�62�ȣ���Ӧ�ɷѶ���Ԫ�������û�ij�½ɷ�105Ԫʱ������û��������˶��ٶȵ磿

���𰸡�������![]()
�������û����õ����ڣ��ȵ�100��֮��ʱ��ÿ�ȵ���շѱ���0.65Ԫ������100��ʱ��ÿ�ȵ���շѱ���0.80Ԫ��
�������û��õ�62��ʱ���û�Ӧ�ɷ�40. 3Ԫ�����û��½ɷ�105Ԫʱ�����û���������150�ȵ磮
��������
������ͼ���֪����0��x��100ʱ���������������������ʽΪy=kx����x��100ʱ�������һ�κ�������ʽΪy=kx+b���������ô���ϵ���������������ʽ��
����ͼ�����õ�����0�ȵ�100��֮��ʱ�����ÿ�ȵ���շѵı������õ�������100��ʱ�����ÿ�ȵ���շѱ���
�ȸ����Ա�����ֵȷ������Ӧ�ĺ�������ʽ���ٴ�����֤����.
�����������1���赱0��x��100ʱ����������ʽΪy=kx��k��0��.
����100��65������y=kx�ã�100k=65�����k=0.65��
��y=0.65x��0��x��100��.
�赱x��100ʱ����������ʽΪy=ax+b��a��0��.
����100��65������130��89������y=kx+b�ã�
![]() ����ã�
����ã�![]() ����y=0.8x-15��x��100��
����y=0.8x-15��x��100��
����y��x�ĺ�����ϵʽΪ![]() ��
��
��2�����ݣ�1���ĺ�����ϵʽ�ã�
���õ�����0�ȵ�100��֮��ʱ��ÿ�ȵ���շѵı���0.65Ԫ�����õ�������100��ʱ��ÿ�ȵ���շѱ���0.8Ԫ��
��3���û����õ�62��ʱ��62��0.65=40.3���û�Ӧ�ɷ�40.3Ԫ��
�û��½ɷ�105Ԫʱ����0.8x-15=105�����x=150�����û���������150�ȵ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
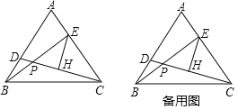
����Ŀ����ͼ���ڵȱ���ABC�У���D����E�ֱ���AB��AC�ϣ�BD=AE������BE��CD���ڵ�P����EH��CD��H��
��1����֤����CAD�ա�BCE����2����֤��PE=2PH����3����PB=PH�����ACD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��B�������ϵ������㣬��A��ʾ����Ϊ��2����B�ڵ�A�Ҳ࣬����A��12����λ���ȣ�����P�ӵ�A��������ÿ��2����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮

��1����գ��������ϵ�B��ʾ����Ϊ�� ����
�������ϵ�P��ʾ����Ϊ�� �����ú�t�Ĵ���ʽ��ʾ����
��2����AP��PB���е�ֱ�Ϊ��M��N���ڵ�P���˶������У��߶�M N�ij����Ƿ����仯�����仯����˵�����ɣ������䣬����߶�M N�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��AOB=��COD,����AOD=110��,��BOC=70��,�����½�����ȷ����(����)

�١�AOC=��BOD=90��;�ڡ�AOB=20��;�ۡ�AOB=��AOD-��AOC;�ܡ�AOB=![]() ��BOD.
��BOD.
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬�ҡ�AFE����B��
��1����֤����ADF�ס�DEC
��2����AB��4��AD��3 ![]() ��AE��3����AF�ij���
��AE��3����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BC=EC����BCE=��ACD�������Ӳ���ʹ��ABC�ա�DBC�������ǣ� ��
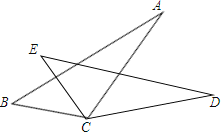
A��AB=DE B����B=��E C��AC=DC D����A=��D
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���ͼͼ�Σ����ǰ�һ���������еģ�����ͼ������ʾ�Ĺ������ǿ��Է��֣���1��ͼ��ʮ����������ǵĸ�����Ϊ7����2��ͼ��ʮ����������ǵĸ�����Ϊ10����3��ͼ��ʮ����������ǵĸ�����Ϊ13�����������Ĺ��ɣ����8��ͼ���У�ʮ����������ǵĸ�����Ϊ��������

A. 25B. 27C. 28D. 31
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y=-![]() x-
x-![]() ��x�ύ�ڵ�A����y�ύ�ڵ�B����C��x���������ϣ���OC=3AO������A��BC��ƽ����l��
��x�ύ�ڵ�A����y�ύ�ڵ�B����C��x���������ϣ���OC=3AO������A��BC��ƽ����l��
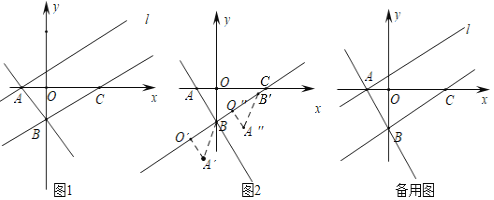
��1����ֱ��BC�Ľ���ʽ��
��2������A����BC�ĶԳƵ�D��һ����P��C�������ijһ·���˶���ֱ��l�ϵĵ�M�����ش�ֱBC�ķ����˶���ֱ��BC�ϵĵ�N������ijһ·���˶���D�㣬���P�˶������·���ij��Լ���ʱ��N�����ꣻ
��3����ͼ2������AOB�Ƶ�B��ת��ʹ��A��O����BC���õ���A��O��B������A��O��B��ֱ��BCƽ�Ƶõ���A��O��B��������A����B����C���Ƿ���ڵ�A����ʹ����A��B��CΪ���������Σ������ڣ���ֱ��д����A�������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=a��x��h��2+k��a��h��kΪ������������ƽ���ϵ�ͼ��ͨ����0��5������15��8�����㣮��a��0��0��h��10����hֵ֮����Ϊ���к�ֵ���� ��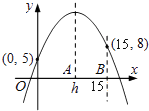
A.5
B.6
C.7
D.8
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com