
【题目】如图1,在平面直角坐标系中,直线y=-![]() x-
x-![]() 与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
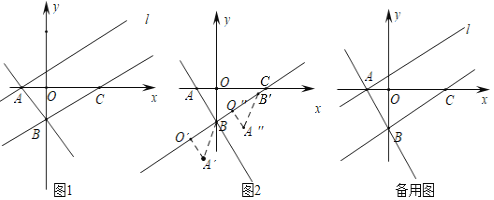
(1)求直线BC的解析式;
(2)作点A关于BC的对称点D,一动点P从C点出发按某一路径运动到直线l上的点M,再沿垂直BC的方向运动到直线BC上的点N,再沿某一路径运动到D点,求点P运动的最短路径的长以及此时点N的坐标;
(3)如图2,将△AOB绕点B旋转,使得A′O′⊥BC,得到△A′O′B,将△A′O′B沿直线BC平移得到△A″O″B′,连接A″、B″、C,是否存在点A″,使得△A″B′C为等腰三角形?若存在,请直接写出点A″的坐标;若不存在,请说明理由.
【答案】(1) y=![]() x-
x-![]() ;(2) 2
;(2) 2![]() , N(
, N(![]() ,-
,-![]() );(3)见解析.
);(3)见解析.
【解析】
(1)利用待定系数法即可解决问题;
(2)如图2中,作点C关于直线AF的对称点C′,连接CC′交AF于点F,连接DF交BC于N,作NE⊥AF于E,连接EC,则此时CE+EN+DN的值最小,最小值=线段DF的长;
(3)分四种情形分别画出图形求解即可.
(1)∵直线y=-![]() x-
x-![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,
∴A(-1,0),B(0,-![]() ),
),
∵OC=3OA,
∴OC=3,
∴C(3,0),
设直线BC的解析式为y=kx+b,则有![]() ,
,
解得 ,
,
∴直线BC的解析式为y=![]() x-
x-![]() ;
;
(2)如图2中,作点C关于直线AF的对称点C′,连接CC′交AF于点F,连接DF交BC于N,作NE⊥AF于E,连接EC,则此时CE+EN+DN的值最小,最小值=线段DF的长.

由题意D(1,-2![]() ),
),
∵直线CF的解析式为y=![]() x+
x+![]() ,直线CF的解析式为y=-
,直线CF的解析式为y=-![]() x+3
x+3![]() ,
,
由 ,解得
,解得![]() ,
,
∴F(2,![]() ),
),
∴DF=![]() =2
=2![]() ,
,
∴点P的路径的最小值为2![]() ,
,
∵直线DF的解析式为y=3![]() x-5
x-5![]() ,
,
由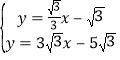 ,解得
,解得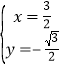 ,
,
∴N(![]() ,-
,-![]() );
);
(3)由题意,BO′=BO=![]() ,AB=BA′=2,OA=O′A′=1,点O′向下平移
,AB=BA′=2,OA=O′A′=1,点O′向下平移![]() 个单位,向右平移
个单位,向右平移![]() 单位得到A′,
单位得到A′,
①如图3中,当CB′=B′A″=2时,此时O″(![]() ,-
,-![]() ),可得A″(2-
),可得A″(2-![]() ,-1-
,-1-![]() ).
).
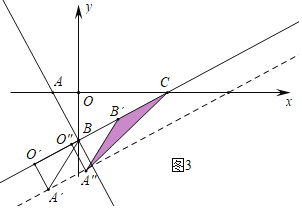
②如图4中,当CB′=CA″时,设CB′=CA″=x,则有x2=12+(![]() -x)2,
-x)2,
可得x=![]() ,此时O″(
,此时O″(![]() ,-
,-![]() ),可得A″(3,-
),可得A″(3,-![]() ).
).
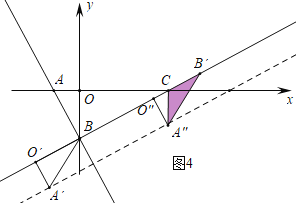
③当B′C=B′A″=2时,O″(![]() ,
,![]() ),可得A″(2+
),可得A″(2+![]() ,1-
,1-![]() )
)
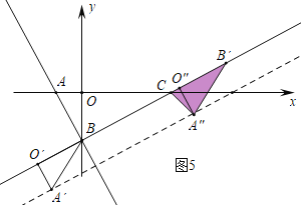
④当CA″=B′A″=2时,O″(![]() ,
,![]() ),可得A″(5,0).
),可得A″(5,0).
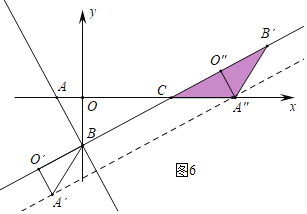
综上所述,满足条件的点A″的坐标为(2-![]() ,-1-
,-1-![]() )或(3,-
)或(3,-![]() )或(2+
)或(2+![]() ,1-
,1-![]() )或(5,0).
)或(5,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
科目:初中数学 来源: 题型:
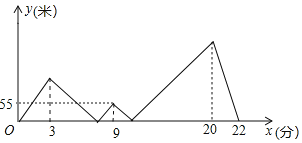
【题目】小明和父亲在一直线公路AB上进行(A→B→A)往返跑训练,两人同时从A点出发,父亲以较快的速度匀速跑到点B休息2分钟后立即原速跑回A点,小明先匀速慢跑了3分钟后,把速度提高到原来的![]() 倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
倍,又经过6分钟后超越了父亲一段距离,小明又将速度降低到出发时的速度,并以这一速度匀速跑到B点看到休息的父亲,然后立即以出发时的速度跑回A点,若两人之间的距离记为y(米),小明的跑步时间记为x(分),y和x的部分函数关系如图所示,则当父亲回到A点时小明距A点______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1 , x2 , 且x1![]() x2有下列结论:①x1=2,x2=3;②m>
x2有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
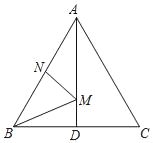
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴,点
轴正半轴,点![]() 在
在![]() 轴负半轴,连接
轴负半轴,连接![]() ,
,![]() ,
,![]()
(1)求点![]() 坐标
坐标
(2)如图2,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为直角边做等腰直角
为直角边做等腰直角![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(3)在(2)的条件下,如图3,在![]() 延长线上有一点
延长线上有一点![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com